Developer’s Guide¶

This is a guide for contributing to the Zelig Project by adding new statistical models into Zelig. Before getting started, familiarize yourself with R’s Reference Classes (RCs), as Zelig5 makes extensive use of RCs to allow for the straightforward addition of new models. Useful resources include Hadley Wickham’s chapter on Reference Classes, and R’s ReferenceClasses documentation. Be sure to read King, Tomz, and Wittenberg (2000) for the underlying algorithm that is deployed in Zelig. Finally, explore zeligproject.org to learn more about Zelig and our plans for the future.

In the abstract, Zelig is a tool for estimating and visualizing easily interpretable quantities of interest for statistical models in R . To do so, Zelig leverages R’s open-source philosophy and builds on existing statistical model implementations such as those found in stats and VGAM. Consider the following R code:

data(turnout)
z5 <- zlogit$new()
z5$zelig(vote ∼ age, data = turnout)
z5$setx()
z5$sim()
z5$graph()

First, we load the data. Then, the next five lines of code are nearly identical for any model in Zelig. The one exception is the first, in which we assign a new model object to z5. zlogit is the RC, and the $ symbol means we are calling a method inside that RC. Each RC is its own environment, and a method is a function that is internal to that environment. Think of the RC as a home, and the method as a room in the home. To enter a room, you must first be inside the home.

z5 is assigned the RC zlogit. new(), zelig(), setx(), sim(), and graph() are all methods inside zlogit and, thus, inside z5. Everything between the parenthesis are arguments passed to the method. zelig() is the method that calls the existing function, which for logistic regression is glm(). The arguments we pass to zelig() are, minimally, the arguments we would pass to glm() if we were to call it directly. zelig() also accepts some arguments that may not be accepted by the existing function, such as by. [1] setx() is a function that sets the predictor values at which we want to simulate. In most implementations, setx() is independent of the model and contributors need not be concerned with it. sim() is the method that simulates draws from the data. For contributors, this is where the model’s link function, or the systematic component, is called. It is also where the relevant quantities of interest are specified. graph() visualizes the output of sim(), and while your model may have visualizations that you’d like to add, these are optional, as graph() has base visualizations that always work on the simulated estimates.

In this guide, we are going to walk through an example with the logit model, as implemented by glm() in the stats library to Zelig. First, let’s download Zelig and load the project in RStudio. This will make it easier to see how the package works in its entirety.

Getting Started¶

Go to RStudio to download and install the latest version of RStudio. Then, go to github.com/IQSS/Zelig and download Zelig.

In the lower right panel of RStudio, click the Files tab, and open Zelig-master, which you just downloaded from Github. Select and load Zelig.Rproj. In the upper right panel, click the Build tab, and then click Build & Reload. This rebuilds the package and loads it into R.

Next, while still in RStudio, in the upper left panel, open the following files, found in Zelig-master/R:

model-zelig.R
model-glm.R
model-binchoice.R
model-logit.R

If you’re new to RStudio or would like to better understand what’s going on, add a print statement and rebuild the package. For example, inside model-zelig.R, find “zelig = function”. This is where the zelig() method is declared. Inside the zelig() method, add a line, cat('Zelig'). Save, and then click Build & Reload in the upper right panel. In the R console:

data(turnout)
z5 <- zlogit$new()
z5$zelig(vote ∼ age, data = turnout)

You should see “Zelig” printed in the console.

Reference Classes and Inheritance¶

RCs have three important properties: (1) they contain fields, (2) they contain methods, and (3) they can inherit fields and methods from other RCs. See the Inheritance Tree at zeligproject.org/models. Notice that Zelig-logit inherits from Zelig-binchoice, Zelig-glm, and Zelig. Each of these nodes in the Inheritance Tree corresponds to a file that we have opened in RStudio.

To contribute a new package, you’ll minimally inherit from Zelig. But, you may extend the inheritance or inherit additional classes, depending on the way your model relates to others. There is no correct answer to inheritance, only what’s logical. Consider logit’s inheritance. Zelig-glm inherits from Zelig, and the glm() function can be used to estimate the following five models: gamma, normal, poisson, probit, and logit. Look at these poisson, logit, and probit estimations:

fit.poisson <- glm(vote ∼ age, data=turnout, family = poisson())
fit.logit <- glm(vote ∼ age, data=turnout, family=binomial("logit"))
fit.probit <- glm(vote ∼ age, data=turnout, family=binomial("probit"))

The family argument is what distinguishes these three estimations, but notice that, while poisson’s family is poisson(), logit’s and probit’s family are both binomial(). So, while poisson may inherit from Zelig-glm and stop there, logit and probit go one step further and inherit from an intermediary class called Zelig-binchoice, which inherits from Zelig-glm.

The Zelig Methods¶

A commonly used implementation of the logistic regression is the glm() function in stats. Load Zelig’s ‘turnout’ data with data(turnout), and estimate 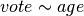$vote \sim age$ using glm():

fit <- glm(vote ∼ age, data=turnout, family=binomial("logit"))

The Zelig counterpart would be:

z5 <- zlogit$new()
z5$zelig(vote ∼ age, data = turnout)

new()¶

We initialize the Zelig object when users enter 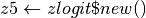$z5 \leftarrow zlogit\$new()$ in the R console. This is when all the information necessary to wrap the logit model using glm() is initialized, and is accomplished using the initialize() method. To understand how the Zelig object is initialized, let’s first explore the inheritance. When we write a RC, we can specify another RC whose fields and methods will be inherited by our RC. Recall logit’s inheritance:

Zelig 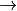$\rightarrow$ Zelig-glm $\rightarrow$ Zelig-binchoice $\rightarrow$ Zelig-logit

Look at the first lines of code in each of the files opened in RStudio, and you’ll see setRefClass(). The chain of inheritance is passed using the contains argument. Starting at the end of the inheritance tree, the RC Zelig-logit contains, or inherits from, the RC Zelig-binchoice, which inherits from the RC Zelig-glm, which inherits from the RC Zelig. In Zelig, we establish our most basic fields and methods, and get more specific as we move down the inheritance.

When zlogit$new() is called, we actually call initialize() first at the end of the inheritance, inside Zelig-logit. Look inside model-logit.R at initialize(). The first line is callSuper(). callSuper() is a method that is common to all RCs, and useful particularly for inheritance. What it does it simple: it calls the same function in the parent object, or the object that the present object inherits from. So, since Zelig-logit inherits from Zelig-binchoice, callSuper() in initialize() calls initialize() inside Zelig-binchoice, where the first command is also callSuper(), and so initialize() is called in Zelig-glm, where the first command is also callSuper(), and so initialize() is called in Zelig. Zelig is at the top of the tree, and so now that we have climbed up the inheritance tree, we next climb down the tree, executing all commands inside initialize() and after callSuper(), first in Zelig, then Zelig-glm, then Zelig-binchoice, and lastly Zelig-logit. See the figure below for a description of this process.

So, to summarize: upon executing 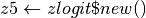$z5 \leftarrow zlogit\$new()$ , we callSuper() inside initialize(), beginning at the end of the inheritance (Zelig-logit) and climbing to the top (Zelig). Then, for each RC, everything below callSuper() inside initialize() is executed, beginning at the top of the inheritance (Zelig) and climbing down (Zelig-logit), assigning the RC’s fields as we descend. For example, in Zelig .self$authors <- "Kosuke Imai, Gary King, and Olivia Lau", and in Zelig-logit, .self$link <- "logit". Doing so initializes our Zelig object, which now waits for zelig() to be called.

zelig()¶

zelig() will help to make sense of why initialize() specifies the fields that it does. Let’s look at zelig() inside model-glm.R, the last RC in the inheritance to modify zelig(). Recall that in initialize(), we started at the bottom of the inheritance, and because the first line is always callSuper(), we climbed to the top before executing any other commands in initialize(). Well, here we don’t callSuper() until later, meaning that the code above callSuper() is execute and then we callSuper() and climb to the parent object. As we descend the inheritance, the code below callSuper() is executed. Let’s have a look at the first lines of code in zelig() in model-glm.R:

.self$zelig.call <- match.call(expand.dots = TRUE)
.self$model.call <- .self$zelig.call

The first command stores the user’s initial zelig() call as it is written by the user. In our example, the field zelig.call would now be z5$zelig(formula = vote ~ age, data = turnout). We now have the user’s call saved as zelig.call. You can see this by entering z5$zelig.call in the R console. Specifically, zelig.call is a field, and we can reach into z5 and pull out the field using the $ operator.

But this is not the call we use to estimate our model, because zelig() is wrapping another function, glm(). To distinguish between the user’s zelig() call and the Zelig object’s glm() call, we copy zelig.call to a new field, model.call. model.call is the field that will be made to appear exactly as if we were to call glm() directly. Thus, if you ever use Zelig and want to know how you would estimate the same model using the package that Zelig wraps, you’ll want to look at the model.call field.

Keep in mind that what we are doing is transforming the initial two user commands into an equivalent form of the glm() call, fit <- glm(vote \sim age, data=turnout, family=binomial(logit)). We are almost there, but still missing the family argument, an essential argument of glm() that must be of class family. This is accomplished with:

.self$model.call$family <- call(.self$family, .self$link)

model.call does not have something called “family” prior to this line of code, so it is created and assigned call(.self$family, .self$link), which is an object of class family. A little confusing, but consider the following example:

myfam <- binomial("logit")

myfam is an object of class family, as returned by binomial("logit"). For the glm() family argument, binomial tells us the type of outcome, and it is stored in the field family. “logit” is the name of the link function, and it is stored in link. Where did .self$family and .self$link come from? Recall the inheritance of initialize(). family is written to our Zelig object in Zelig-binchoice, and link is written to our Zelig object in Zelig-logit. So, model.call is now:

z5$zelig(formula = vote ∼ age, data = turnout, family = binomial("logit"))

If we want to specify a different link function, e.g., probit, then all we would have to change is .self$link <- logit to .self$link <- probit. In fact, in Zelig’s probit model, this is the only functional difference. A couple other things are changed for descriptive purposes, such as the name to “probit”, but functionally, the difference is the link field. And, indeed, in a call to glm(), logit and probit appear identical with the exception of the binomial argument, which is either “logit” or “probit”.

Lastly, we callSuper(). Recall that this is a method that is common to all RCs; it calls the method of the same name in the object that this object inherits from. So, after assigning zelig.call and model.call, we call zelig() in Zelig to actually compute the estimation.

Next, let’s look at the zelig() method inside Zelig, seen in the model-zelig.R script. When contributing to Zelig, model-zelig.R should never be altered.

This method is very dense, and includes code for working with multiple datasets (e.g., those from Amelia) and the by argument, among other things. Let’s focus on Zelig’s logit model-the remainder of this section is only concerned with code in zelig() explicitly related to estimating a single logit model from a single dataset. Specifically, look at:

.self$model.call[[1]] <- .self$fn

.self$model.call is a call, and the element indexed by [[1]] is literally the name of the function to be called. For example, call(sum, c(1,1,3)) would return an object of type call that looks exactly like the string sum(c(1,1,3)), but contains elements that can be used to manipulate pieces of the string. Consider the following:

t <- call("sum", c(1,1,3))
eval(t)
t[[1]] <- quote(prod)
eval(t)

The first eval(t) returns 5, the sum of the elements (1,1,3). The second eval(t) returns 3, the product of the elements (1,1,3). [2] In zelig(), the element of model.call we are manipulating is at [[1]], and it is the function to be called. Or, more precisely, it is whatever precedes the first open parenthesis. So, prior to assigning .self$fn to .self$model.call[[1]], the function to be called is z5$zelig, and model.call looks like:

z5$zelig(formula = vote ∼ age, data = turnout, family = binomial("logit"))

After assigning .self$fn to model.call[[1]], model.call looks like:

stats::glm(formula = vote ∼ age, data = turnout, family = binomial("logit"))

The final line of code that we are concerned with is the final line in zelig(), where model.call is evaluated:

do(z.out = eval(fn2(.self$model.call, quote(.))))

Ignore do() and fn2(), these are functions that help us handle multiple datasets, and are part of Zelig’s added value that comes free. All we are doing here is evaluating model.call, which, as is seen above, is now identical to the glm() call. Thus, we have wrapped glm() and estimated a logit model in the Zelig framework.

sim()¶

King, Tomz, and Wittenberg (2000) present a general framework for simulating easily interpretable quantities of interest. We first set our predictor values at which we want to simulate, and then we simulate the quantities of interest, e.g., expected values, predicted values, and first differences. There are two simple Zelig commands to do this:

z5$setx()
z5$sim()

setx() is typically independent of the model, and so we are not concerned with its workings here. For now, suffice to say that on setx(), there is a boolean field called bsetx that is assigned TRUE. sim(), on the other hand, is very much dependent on the model, and so this section describes sim() in detail.

There are four methods that are relevant to sim(), and they are executed in this order:

sim() defined in Zelig
param() defined in Zelig-glm
simx() defined in Zelig
qi() defined in Zelig-binchoice

sim() calls param(), and later simx(). param() returns a matrix of draws from a multivariate normal via the following:

return(mvrnorm(.self$num, coef(z.out), vcov(z.out)))

Recall that the z.out field is equivalent to fit in 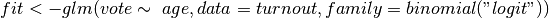$fit <- glm(vote \sim\ age, data=turnout, family=binomial("logit"))$ . .self$num specifies the number of samples taken from the multivariate normal distribution. Inside sim(), the field simparam is assigned the matrix returned by param(). Next, simx() is called, which assigns appropriate covariate values to mm, and then calls qi(), a method whose arguments are a matrix of simulated parameters (simparam) and a set of covariate values (mm).

That is important: qi() is a method whose arguments are a matrix of simulated parameters (simparam) and a set of covariate values (mm). qi() is the real workhorse method when we use sim(), and will likewise be the workhorse for any contributes models. Let’s walk through it line by line. The qi() method is written in Zelig-binchoice.

.self$linkinv <- eval(call(.self$family, .self$link))$linkinv

This is the first, and one of the more important, lines of code. Here is where we assign the linkinv field, which is the inverse of the logit link function. We know that .self$family is “binomial” and .self$link is “logit”, so perhaps this line is a bit easier to read like this: .self$linkinv <- eval(call(binomial, logit))$linkinv. Recall that we have seen call(.self$family, .self$link) before, when we assigned it to the family field in our Zelig object. Recall that it evaluates to an object of class family, and, in our logit example, is equivalent to entering binomial(logit) into the R console.

Only now we don’t want a family object, but we want the inverse of the link function, which is contained inside the family object. Hence, from our family object, we reach in and grab linkinv (via $linkinv), and assign it to the linkinv field in our Zelig object. linkinv is a function, specifically, the inverse of the link function. For your model, this function may not exist, and may need to be written separately.

Just for clarification, enter the following in your R console, which is an R function that returns the inverse of the logit link:

L <- function(m) {
    return (1-(1/(1+exp(m))))
}

Next, enter L(.5). Now enter z5$linkinv(.5). The values returned will be identical. Try it with any value you like. This will work exactly the same way, with a different link function of course, regardless of which Zelig model is selected. Look at the next three lines in qi():

coeff <- simparam
eta <- simparam %*% t(mm)
eta <- Filter(function (y) !is.na(y), eta)

coeff is a copy of simparam, and eta is the matrix multiplication of simparam and mm, which produces a matrix of dimension nrow(simparam) \times 1. By default, nrow(simparam) is 1000. The final line drops any NAs in eta, and coerces the object from a matrix of one column to a numerical vector.

theta <- matrix(.self$linkinv(eta), nrow = nrow(coeff))
ev <- matrix(.self$linkinv(eta), ncol = ncol(theta))
pv <- matrix(nrow = nrow(ev), ncol = ncol(ev)).

Here, we construct a 1000x1 matrix and assign it to theta. .self$linkinv(eta) is simply the inverse link applied to each value in the eta vector, and this fills in the values of the theta matrix. The number of rows in the matrix theta are the number of simulations, or the number of rows in the matrix of simulated parameters. ev and pv have a number of rows equal to the number of observations in eta after NAs are dropped, and a number of columns equal to 1.

for (j in 1:ncol(ev))
    pv[, j] <- rbinom(length(ev[, j]), 1, prob = ev[, j])
return(list(ev = ev, pv = pv))

Next, we iterate over the columns in the ev matrix, and assign predicted values one column at a time. For the default number of simulations (1000) and the logit, this is 1000 draws from a binomial distribution, each with a trial size of 1 and a probability of drawing 1 equal to the value in the corresponding cell in the $j^{th}$ column of ev. Lastly, we return a list with two objects, each a matrix, holding our expected values and predicted values.

Now we have our function that simulates the quantities of interest. These quantities of interest, and the model estimates, are the primary components used in Zelig’s various plot, accessible with z5$graph().

[1]	See the Zelig documentation for more details.

[2]	quote(expr) returns the expression `expr`.