Gamma Survey

Built using Zelig version 5.1.4.90000

Gamma Regression for Continuous, Positive Dependent Variables with gamma.survey.

Use the gamma regression model if you have a positive-valued dependent variable such as the number of years a parliamentary cabinet endures, or the seconds you can stay airborne while jumping. The gamma distribution assumes that all waiting times are complete by the end of the study (censoring is not allowed).

Syntax

z.out <- zelig(Y ~ X1 + X2, model = "gamma.survey", weights = w, data = mydata)
x.out <- setx(z.out)
s.out <- sim(z.out, x = x.out, x1 = NULL)

Examples

Example 1: User has Existing Sample Weights

Attach sample data and variable names:

data(api, package="survey")

In this example, we will estimate a model using the percentages of students who receive subsidized lunch and an indicator for whether schooling is year-round to predict California public schools’ academic performance index scores:

z.out1 <- zelig(api00 ~ meals + yr.rnd, model = "gamma.survey",
                weights = ~pw, data = apistrat)

## Warning: Not all features are available in Zelig Survey.
## Consider using surveyglm and setx directly.
## For details see: <http://docs.zeligproject.org/articles/to_zelig.html>.

## How to cite this model in Zelig:
##   Nicholas Carnes. 2017.
##   gamma-survey: Gamma Regression with Survey Weights
##   in Christine Choirat, Christopher Gandrud, James Honaker, Kosuke Imai, Gary King, and Olivia Lau,
##   "Zelig: Everyone's Statistical Software," http://zeligproject.org/

summary(z.out1)

## Model: 
## 
## Call:
## z5$zelig(formula = api00 ~ meals + yr.rnd, data = apistrat, weights = ~pw)
## 
## Survey design:
## survey::svydesign(data = data, ids = ids, probs = probs, strata = strata, 
##     fpc = fpc, nest = nest, check.strata = check.strata, weights = localWeights)
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.128e-03  1.560e-05  72.314   <2e-16
## meals       7.928e-06  4.391e-07  18.056   <2e-16
## yr.rndYes   5.113e-05  4.449e-05   1.149    0.252
## 
## (Dispersion parameter for Gamma family taken to be 0.3836199)
## 
## Number of Fisher Scoring iterations: 4
## 
## Next step: Use 'setx' method

Set explanatory variables to their default (mean/mode) values, and set a high (80th percentile) and low (20th percentile) value for “meals,” the percentage of students who receive subsidized meals:

x.low <- setx(z.out1, meals= quantile(apistrat$meals, 0.2))
x.high <- setx(z.out1, meals= quantile(apistrat$meals, 0.8))

Generate first differences for the effect of high versus low “meals” on academic performance:

s.out1 <- sim(z.out1, x=x.high, x1=x.low)
summary(s.out1)

## 
##  sim x :
##  -----
## ev
##          mean       sd      50%     2.5%    97.5%
## [1,] 582.7601 7.921319 582.6495 568.0145 598.4627
## pv
##          mean       sd      50%     2.5%    97.5%
## [1,] 580.7022 372.2473 499.5856 101.8357 1529.045
## 
##  sim x1 :
##  -----
## ev
##          mean       sd      50%     2.5%    97.5%
## [1,] 786.7721 6.821552 786.6617 773.1634 800.1334
## pv
##          mean       sd     50%     2.5%    97.5%
## [1,] 778.3914 505.7795 675.047 124.1773 1958.094
## fd
##         mean       sd      50%     2.5%    97.5%
## [1,] 204.012 9.939606 203.8514 184.0507 223.0171

Generate a second set of fitted values and a plot:

plot(s.out1)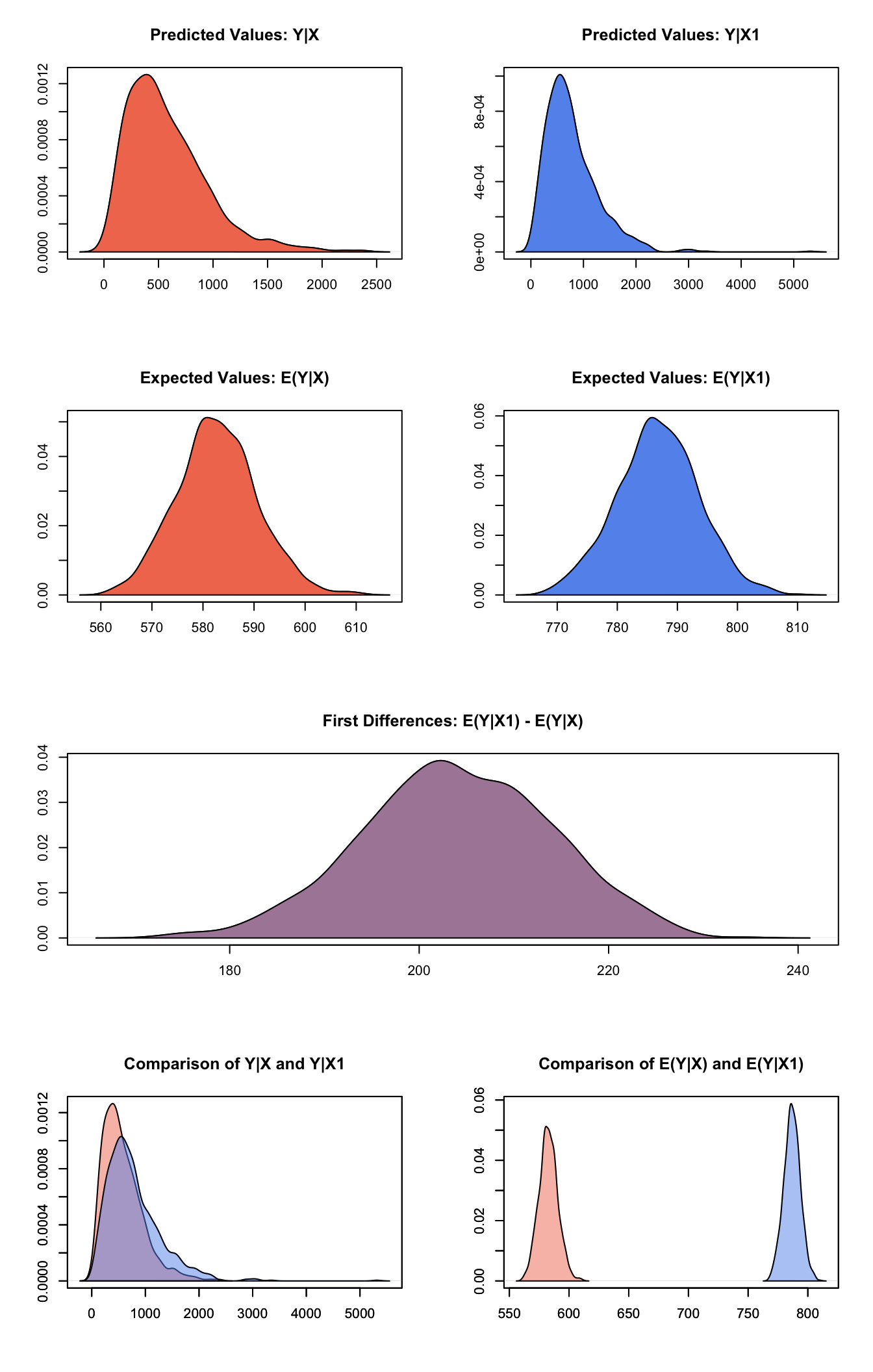

Graphs of Quantities of Interest for Gamma Survey

Example 2: User has Details about Complex Survey Design (but not sample weights)

Suppose that the survey house that provided the dataset excluded probability weights but made other details about the survey design available. We can still estimate a model without probability weights that takes instead variables that identify each the stratum and/or cluster from which each observation was selected and the size of the finite sample from which each observation was selected.

z.out2 <- zelig(api00 ~ meals + yr.rnd, model = "gamma.survey",
                strata=~stype, fpc=~fpc, data = apistrat)

## Warning: Not all features are available in Zelig Survey.
## Consider using surveyglm and setx directly.
## For details see: <http://docs.zeligproject.org/articles/to_zelig.html>.

## How to cite this model in Zelig:
##   Nicholas Carnes. 2017.
##   gamma-survey: Gamma Regression with Survey Weights
##   in Christine Choirat, Christopher Gandrud, James Honaker, Kosuke Imai, Gary King, and Olivia Lau,
##   "Zelig: Everyone's Statistical Software," http://zeligproject.org/

summary(z.out2)

## Model: 
## 
## Call:
## z5$zelig(formula = api00 ~ meals + yr.rnd, data = apistrat, strata = ~stype, 
##     fpc = ~fpc)
## 
## Survey design:
## survey::svydesign(data = data, ids = ids, probs = probs, strata = strata, 
##     fpc = fpc, nest = nest, check.strata = check.strata, weights = localWeights)
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.162e-03  1.472e-05  78.980   <2e-16
## meals       7.859e-06  4.276e-07  18.380   <2e-16
## yr.rndYes   2.807e-05  4.392e-05   0.639    0.523
## 
## (Dispersion parameter for Gamma family taken to be 0.01251498)
## 
## Number of Fisher Scoring iterations: 4
## 
## Next step: Use 'setx' method

Note that these results are identical to the results obtained when pre-existing sampling weights were used. When sampling weights are omitted, Zelig estimates them automatically for “gamma.survey” models based on the user-defined description of sampling designs. If no description is present, the default assumption is equal probability sampling.

The methods setx()`` andsim()can then be run onz.out2` in the same fashion described in Example 1.

Example 3: User has Replicate Weights

Suppose that the survey house that published these data withheld details about the survey design and instead published replication weights.

For the purpose of illustration, create a set of jk1 replicate weights:

library("survey")

## Loading required package: grid

## Loading required package: Matrix

## 
## Attaching package: 'survey'

## The following object is masked from 'package:graphics':
## 
##     dotchart

jk1reps <- jk1weights(psu=apistrat$dnum)

Estimate the model regressing api00 on the “meals” “yr.rnd” variables.

z.out3 <- zelig(api00 ~ meals + yr.rnd, model = "gamma.survey",
      data = apistrat, repweights=jk1reps$weights,
      type="JK1")

## Warning: Not all features are available in Zelig Survey.
## Consider using surveyglm and setx directly.
## For details see: <http://docs.zeligproject.org/articles/to_zelig.html>.

## How to cite this model in Zelig:
##   Nicholas Carnes. 2017.
##   gamma-survey: Gamma Regression with Survey Weights
##   in Christine Choirat, Christopher Gandrud, James Honaker, Kosuke Imai, Gary King, and Olivia Lau,
##   "Zelig: Everyone's Statistical Software," http://zeligproject.org/

summary(z.out3)

## Model: 
## 
## Call:
## z5$zelig(formula = api00 ~ meals + yr.rnd, data = apistrat, repweights = jk1reps$weights, 
##     type = "JK1")
## 
## Survey design:
## survey::svydesign(data = data, ids = ids, probs = probs, strata = strata, 
##     fpc = fpc, nest = nest, check.strata = check.strata, weights = localWeights)
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)
## (Intercept)  1.210e-03  1.858e-05  65.146   <2e-16
## meals        7.868e-06  4.658e-07  16.891   <2e-16
## yr.rndYes   -6.263e-06  4.639e-05  -0.135    0.893
## 
## (Dispersion parameter for Gamma family taken to be 0.01458664)
## 
## Number of Fisher Scoring iterations: 4
## 
## Next step: Use 'setx' method

Set the explanatory variable “meals” at high and low values

x.low <- setx(z.out3, meals= quantile(apistrat$meals, 0.2))
x.high <- setx(z.out3, meals= quantile(apistrat$meals, 0.8))

Generate first differences for the effect of the high versus low concentrations of poverty on school performance

s.out3 <- sim(z.out3, x=x.high, x1=x.low)
summary(s.out3)

## 
##  sim x :
##  -----
## ev
##          mean     sd     50%     2.5%    97.5%
## [1,] 557.7079 7.9431 557.529 542.4628 573.5257
## pv
##          mean      sd      50%     2.5%    97.5%
## [1,] 555.9965 69.3922 553.1337 425.1246 700.4409
## 
##  sim x1 :
##  -----
## ev
##          mean       sd      50%     2.5%    97.5%
## [1,] 739.7963 7.695778 739.8023 725.4739 755.3309
## pv
##          mean       sd      50%     2.5%    97.5%
## [1,] 742.6941 88.52467 740.4528 571.1378 921.2419
## fd
##          mean       sd      50%     2.5%    97.5%
## [1,] 182.0884 10.23062 181.9744 162.3653 201.8603

Generate a second set of fitted values and a plot:

plot(s.out3)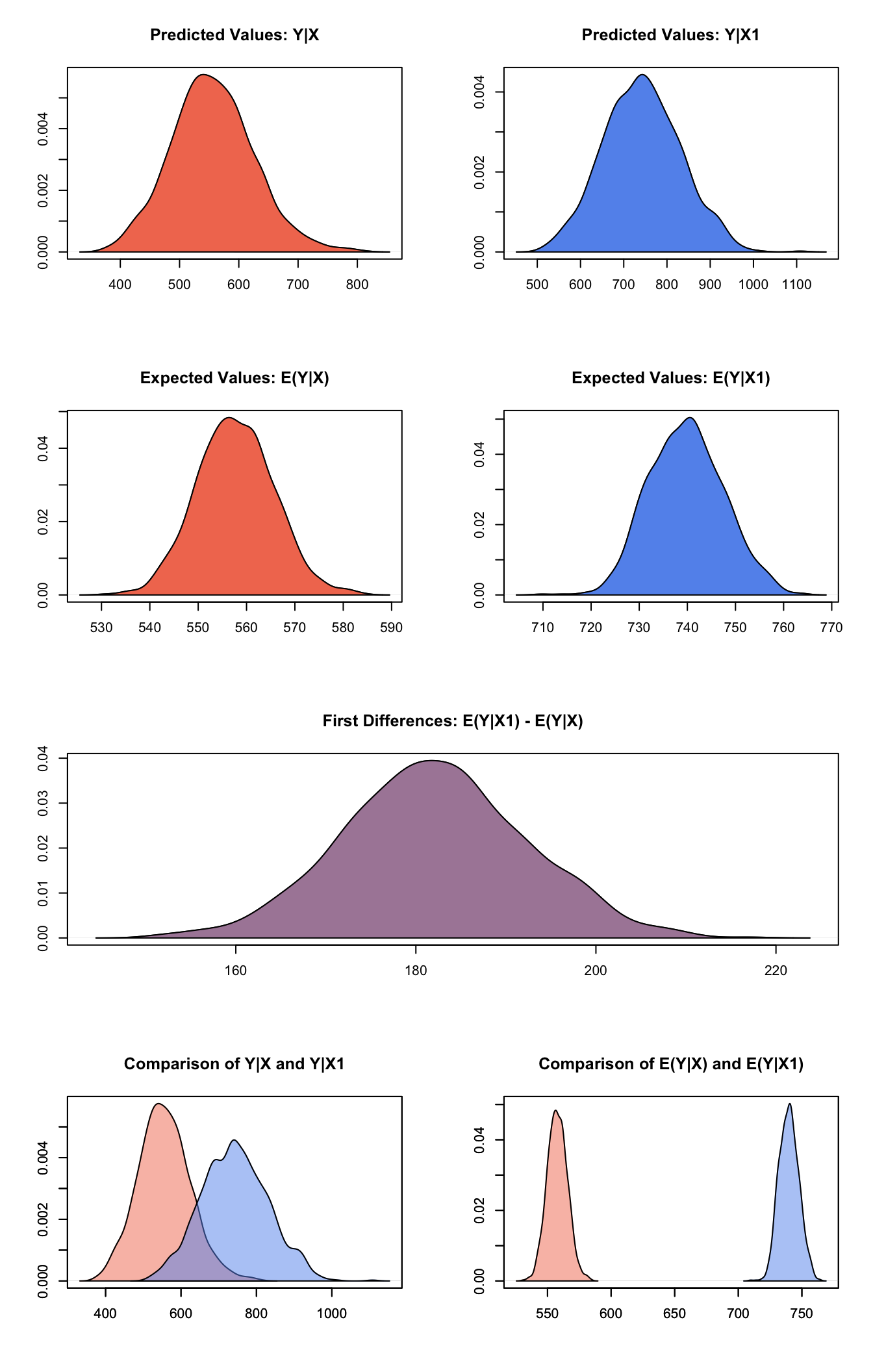

The user should also refer to the gamma model demo, since gamma.survey models can take many of the same options as gamma models.

Model

The Gamma distribution with scale parameter $\alpha$ has a stochastic component:

\[ \begin{aligned} Y &\sim& \textrm{Gamma}(y_i \mid \lambda_i, \alpha) \\ f(y) &=& \frac{1}{\alpha^{\lambda_i} \, \Gamma \lambda_i} \, y_i^{\lambda_i - 1} \exp -\left\{ \frac{y_i}{\alpha} \right\}\end{aligned} \] | for $\alpha, \lambda_i, y_i > 0$.

The systematic component is given by

\[ \lambda_i = \frac{1}{x_i \beta} \]

Quantities of Interest

The expected values (qi$ev) are simulations of the mean of the stochastic component given draws of $\alpha$ and $\beta$ from their posteriors:

\[ E(Y) = \alpha \lambda_i. \]

The predicted values (qi$pr) are draws from the gamma distribution for each given set of parameters $(\alpha, \lambda_i)$.
If x1 is specified, sim() also returns the differences in the expected values (qi$fd),

\[ E(Y \mid x_1) - E(Y \mid x) \]

In conditional prediction models, the average expected treatment effect (att.ev) for the treatment group is

\[ \frac{1}{\sum_{i=1}^n t_i}\sum_{i:t_i=1}^n \left\{ Y_i(t_i=1) - E[Y_i(t_i=0)] \right\}, \]

where $t_i$ is a binary explanatory variable defining the treatment ($t_i=1$) and control ($t_i=0$) groups. Variation in the simulations are due to uncertainty in simulating $E[Y_i(t_i=0)]$, the counterfactual expected value of $Y_i$ for observations in the treatment group, under the assumption that everything stays the same except that the treatment indicator is switched to $t_i=0$.

In conditional prediction models, the average predicted treatment effect (att.pr) for the treatment group is

\[ \frac{1}{\sum_{i=1}^n t_i}\sum_{i:t_i=1}^n \left\{ Y_i(t_i=1) - \widehat{Y_i(t_i=0)} \right\}, \]

where $t_i$ is a binary explanatory variable defining the treatment ($t_i=1$) and control ($t_i=0$) groups. Variation in the simulations are due to uncertainty in simulating $\widehat{Y_i(t_i=0)}$, the counterfactual predicted value of $Y_i$ for observations in the treatment group, under the assumption that everything stays the same except that the treatment indicator is switched to $t_i=0$.

Output Values

The Zelig object stores fields containing everything needed to rerun the Zelig output, and all the results and simulations as they are generated. In addition to the summary commands demonstrated above, some simply utility functions (known as getters) provide easy access to the raw fields most commonly of use for further investigation.

In the example above z.out$get_coef() returns the estimated coefficients, z.out$get_vcov() returns the estimated covariance matrix, and z.out$get_predict() provides predicted values for all observations in the dataset from the analysis.

2017-10-29