zelig-normalbayes¶

Bayesian Normal Linear Regression

Use Bayesian regression to specify a continuous dependent variable as a linear function of specified explanatory variables. The model is implemented using a Gibbs sampler. See for the maximum-likelihood implementation or for the ordinary least squares variation.

Syntax¶

z5 <- znormalbayes$new()
z5$zelig(Y ~ X1 + X2, weights = w, data = mydat)
z5$setx()
z5$sim()

With the Zelig 4 compatibility wrappers:

z.out <- zelig(Y ~ X1 + X2, model = "normal.bayes", weights = w, data = mydata)
x.out <- setx(z.out)
s.out <- sim(z.out, x = x.out)

Additional Inputs¶

Use the following arguments to monitor the convergence of the Markov chain:

burnin: number of the initial MCMC iterations to be discarded (defaults to 1,000).
mcmc: number of the MCMC iterations after burnin (defaults to 10,000).
thin: thinning interval for the Markov chain. Only every thin-th draw from the Markov chain is kept. The value of mcmc must be divisible by this value. The default value is 1.
verbose: defaults to FALSE. If TRUE, the progress of the sampler (every ) is printed to the screen.
seed: seed for the random number generator. The default is NA, which corresponds to a random seed of 12345.
beta.start: starting values for the Markov chain, either a scalar or vector with length equal to the number of estimated coefficients. The default is NA, which uses the least squares estimates as the starting values.

Use the following arguments to specify the model’s priors:

b0: prior mean for the coefficients, either a numeric vector or a scalar. If a scalar, that value will be the prior mean for all the coefficients. The default is 0.
B0: prior precision parameter for the coefficients, either a square matrix (with the dimensions equal to the number of the coefficients) or a scalar. If a scalar, that value times an identity matrix will be the prior precision parameter. The default is 0, which leads to an improper prior.
c0: c0/2 is the shape parameter for the Inverse Gamma prior on the variance of the disturbance terms.
d0: d0/2 is the scale parameter for the Inverse Gamma prior on the variance of the disturbance terms.

Zelig users may wish to refer to help(MCMCregress) for more information.

Examples¶

Basic Example¶

Attaching the sample dataset:

data(macro)

Estimating linear regression using normal.bayes:

z.out <- zelig(unem ~ gdp + capmob + trade, model = "normal.bayes",
               data = macro, verbose = FALSE)

## Warning in readLines(zeligmixedmodels): incomplete final line found on
## '/usr/lib64/R/library/ZeligMultilevel/JSON/zelig5mixedmodels.json'

## How to cite this model in Zelig:
##   Ben Goodrich, and Ying Lu. 2013.
##   normal-bayes: Bayesian Normal Linear Regression
##   in Christine Choirat, Christopher Gandrud, James Honaker, Kosuke Imai, Gary King, and Olivia Lau,
##   "Zelig: Everyone's Statistical Software," http://zeligproject.org/

You can check for convergence before summarizing the estimates with three diagnostic tests. See the section Diagnostics for Zelig Models for examples of the output with interpretation:

z.out$geweke.diag()
z.out$heidel.diag()
z.out$raftery.diag()

summary(z.out)

## Model:
##
## Iterations = 1001:11000
## Thinning interval = 1
## Number of chains = 1
## Sample size per chain = 10000
##
## 1. Empirical mean and standard deviation for each variable,
##    plus standard error of the mean:
##
##                Mean      SD Naive SE Time-series SE
## (Intercept)  6.1773 0.45148 4.51e-03       4.51e-03
## gdp         -0.3240 0.06349 6.35e-04       6.35e-04
## capmob       1.4207 0.16562 1.66e-03       1.66e-03
## trade        0.0199 0.00561 5.61e-05       5.37e-05
## sigma2       7.5834 0.57846 5.78e-03       5.96e-03
##
## 2. Quantiles for each variable:
##
##                 2.5%     25%    50%     75%   97.5%
## (Intercept)  5.30927  5.8707  6.180  6.4779  7.0878
## gdp         -0.45044 -0.3669 -0.324 -0.2812 -0.2012
## capmob       1.09273  1.3105  1.422  1.5335  1.7461
## trade        0.00873  0.0162  0.020  0.0237  0.0308
## sigma2       6.53464  7.1766  7.553  7.9552  8.7957
##
## Next step: Use 'setx' method

Setting values for the explanatory variables to their sample averages:

x.out <- setx(z.out)

Simulating quantities of interest from the posterior distribution given x.out:

s.out1 <- sim(z.out, x = x.out)
summary(s.out1)

##
##  sim x :
##  -----
## ev
##   mean    sd  50% 2.5% 97.5%
## 1 4.99 0.148 4.99 4.71  5.28
## pv
##      mean   sd  50%  2.5% 97.5%
## [1,] 5.01 2.72 5.01 -0.29  10.3

Simulating First Differences¶

Set explanatory variables to their default(mean/mode) values, with high (80th percentile) and low (20th percentile) trade on GDP:

x.high <- setx(z.out, trade = quantile(macro$trade, prob = 0.8))
x.low <- setx(z.out, trade = quantile(macro$trade, prob = 0.2))

Estimating the first difference for the effect of high versus low trade on unemployment rate:

s.out2 <- sim(z.out, x = x.high, x1 = x.low)
summary(s.out2)

##
##  sim x :
##  -----
## ev
##   mean    sd  50% 2.5% 97.5%
## 1 5.43 0.192 5.43 5.06  5.81
## pv
##      mean   sd  50%  2.5% 97.5%
## [1,] 5.41 2.78 5.44 0.038  10.9
##
##  sim x1 :
##  -----
## ev
##   mean    sd 50% 2.5% 97.5%
## 1  4.6 0.185 4.6 4.24  4.97
## pv
##      mean   sd 50%   2.5% 97.5%
## [1,] 4.61 2.76 4.6 -0.768    10
## fd
##     mean    sd    50%  2.5%  97.5%
## 1 -0.833 0.235 -0.836 -1.29 -0.365

Model¶

The stochastic component is given by

where .
The systematic component is given by

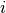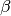where is the vector of explanatory variables for observation $i$ and $\beta$ is the vector of coefficients.
The semi-conjugate priors for 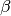$\beta$ and are given by

where is the vector of means for the explanatory variables, is the precision matrix (the inverse of a variance-covariance matrix), and and are the shape and scale parameters for . Note that 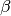$\beta$ and are assumed to be a priori independent.

Quantities of Interest¶

The expected values (qi$ev) for the linear regression model are calculated as following:

given posterior draws of 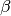$\beta$ based on the MCMC iterations.
The first difference (qi$fd) for the linear regression model is defined as
In conditional prediction models, the average expected treatment effect (qi$att.ev) for the treatment group is

where is a binary explanatory variable defining the treatment () and control () groups.
In conditional prediction models, the average predicted treatment effect (att.pr) for the treatment group is

where is a binary explanatory variable defining the treatment () and control () groups.

Output Values¶

The output of each Zelig command contains useful information which you may view. For example, if you run:

z.out <- zelig(y ~ x, model = "normal.bayes", data)

then you may examine the available information in z.out by using names(z.out), see the draws from the posterior distribution of the coefficients by using z.out$coefficients, and view a default summary of information through summary(z.out). Other elements available through the $ operator are listed below.

From the zelig() output object z.out, you may extract:
- coefficients: draws from the posterior distributions of the estimated parameters. The first columns contain the posterior draws of the coefficients 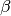$\beta$ , and the last column contains the posterior draws of the variance .
- zelig.data: the input data frame if save.data = TRUE.
- seed: the random seed used in the model.
From the sim() output object s.out:
- qi$ev: the simulated expected values for the specified values of x.
- qi$fd: the simulated first difference in the expected values for the values specified in x and x1.
- qi$att.ev: the simulated average expected treatment effect for the treated from conditional prediction models.