zeligchoice-mlogit¶
Multinomial Logistic Regression for Dependent Variables with Unordered Categorical Values
Use the multinomial logit distribution to model unordered categorical variables. The dependent variable may be in the format of either character strings or integer values. See for a Bayesian version of this model.
Syntax¶
First load packages:
library("Zelig")
library("ZeligChoice")
With reference classes:
z5 <- zmlogit$new()
z5$zelig(as.factor(Y) ~ X1 + X2, data = mydata)
z5$setx()
z5$sim()
With the Zelig 4 compatibility wrappers:
z.out <- zelig(as.factor(Y) ~ X1 + X23,
model = "mlogit", data = mydata)
x.out <- setx(z.out)
s.out <- sim(z.out, x = x.out, x1 = NULL)
where Y above is supposed to be a factor variable with levels apples,bananas,oranges. By default, oranges is the last level and omitted. (You cannot specify a different base level at this time.) For equations, there must be levels.
Examples¶
Load the sample data:
data(mexico)
Estimate the empirical model:
z.out1 <- zelig(as.factor(vote88) ~ pristr + othcok + othsocok,
model = "mlogit", data = mexico)
## Warning in readLines(zeligmixedmodels): incomplete final line found on
## '/usr/lib64/R/library/ZeligMultilevel/JSON/zelig5mixedmodels.json'
## How to cite this model in Zelig:
## Thomas W. Yee. 2007.
## mlogit: Multinomial Logistic Regression for Dependent Variables with Unordered Categorical Values
## in Christine Choirat, Christopher Gandrud, James Honaker, Kosuke Imai, Gary King, and Olivia Lau,
## "Zelig: Everyone's Statistical Software," http://zeligproject.org/
Summarize estimated paramters:
summary(z.out1)
## Model:
##
## Call:
## z5$zelig(formula = as.factor(vote88) ~ pristr + othcok + othsocok,
## data = mexico)
##
##
## Pearson residuals:
## Min 1Q Median 3Q Max
## log(mu[,1]/mu[,3]) -4.30 -0.687 0.279 0.7019 2.10
## log(mu[,2]/mu[,3]) -2.25 -0.469 -0.208 -0.0887 4.54
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept):1 2.8708 0.3964 7.24 4.4e-13
## (Intercept):2 0.3992 0.4701 0.85 0.396
## pristr:1 0.5969 0.0912 6.54 6.1e-11
## pristr:2 -0.1250 0.1043 -1.20 0.231
## othcok:1 -1.2426 0.1124 -11.06 < 2e-16
## othcok:2 -0.1407 0.1330 -1.06 0.290
## othsocok:1 -0.3026 0.1496 -2.02 0.043
## othsocok:2 0.0498 0.1610 0.31 0.757
##
## Number of linear predictors: 2
##
## Names of linear predictors: log(mu[,1]/mu[,3]), log(mu[,2]/mu[,3])
##
## Residual deviance: 2361 on 2710 degrees of freedom
##
## Log-likelihood: -1180 on 2710 degrees of freedom
##
## Number of iterations: 4
##
## Reference group is level 3 of the response
## Next step: Use 'setx' method
Set the explanatory variables to their default values, with pristr (for the strength of the PRI) equal to 1 (weak) in the baseline values, and equal to 3 (strong) in the alternative values:
x.weak <- setx(z.out1, pristr = 1)
x.strong <- setx(z.out1, pristr = 3)
Generate simulated predicted probabilities qi$ev and differences in the predicted probabilities qi$fd:
s.out.mlogit <- sim(z.out1, x = x.strong, x1 = x.weak)
summary(s.out.mlogit)
##
## sim x :
## -----
## ev
## mean sd 50% 2.5% 97.5%
## Pr(Y=1) 0.714 0.0212 0.715 0.670 0.752
## Pr(Y=2) 0.128 0.0148 0.127 0.101 0.160
## Pr(Y=3) 0.158 0.0164 0.158 0.128 0.193
## pv
## 1 2 3
## [1,] 0.708 0.13 0.162
##
## sim x1 :
## -----
## ev
## mean sd 50% 2.5% 97.5%
## Pr(Y=1) 0.402 0.0217 0.403 0.359 0.444
## Pr(Y=2) 0.305 0.0217 0.305 0.265 0.350
## Pr(Y=3) 0.293 0.0211 0.292 0.254 0.337
## pv
## 1 2 3
## [1,] 0.408 0.286 0.306
## fd
## mean sd 50% 2.5% 97.5%
## Pr(Y=1) -0.312 0.0330 -0.312 -0.3734 -0.247
## Pr(Y=2) 0.177 0.0276 0.177 0.1243 0.231
## Pr(Y=3) 0.135 0.0280 0.135 0.0782 0.188
plot(s.out.mlogit)
Graphs of Quantities of Interest for Multinomial Logit
Model¶
Let be the unordered categorical dependent variable that takes one of the values from 1 to , where is the total number of categories.
The stochastic component is given by
where for .
The systemic component is given by:
where is the vector of explanatory variables for observation
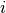 , and is the vector of
coefficients for category .
, and is the vector of
coefficients for category .
Quantities of Interest¶
The expected value (qi$ev) is the predicted probability for each category:
The predicted value (qi$pr) is a draw from the multinomial distribution defined by the predicted probabilities.
The first difference in predicted probabilities (qi$fd), for each category is given by:
In conditional prediction models, the average expected treatment effect (att.ev) for the treatment group is
where is a binary explanatory variable defining the treatment () and control () groups, and is the number of treated observations in category .
In conditional prediction models, the average predicted treatment effect (att.pr) for the treatment group is
where is a binary explanatory variable defining the treatment () and control () groups, and is the number of treated observations in category .
Output Values¶
The output of each Zelig command contains useful information which you may view. For example, if you run z.out <- zelig(y ~ x, model = mlogit, data), then you may examine the available information in z.out by using names(z.out), see the coefficients by using z.out$coefficients, and a default summary of information through summary(z.out). Other elements available through the $ operator are listed below.
- From the zelig() output object z.out, you may extract:
- coefficients: the named vector of coefficients.
- fitted.values: an matrix of the in-sample fitted values.
- predictors: an matrix of the linear predictors .
- residuals: an matrix of the residuals.
- df.residual: the residual degrees of freedom.
- df.total: the total degrees of freedom.
- rss: the residual sum of squares.
- y: an matrix of the dependent variables.
- zelig.data: the input data frame if save.data = TRUE.
- From summary(z.out), you may extract:
- coef3: a table of the coefficients with their associated standard errors and -statistics.
- cov.unscaled: the variance-covariance matrix.
- pearson.resid: an matrix of the Pearson residuals.
See also¶
The multinomial logit function is part of the VGAM package by Thomas Yee. In addition, advanced users may wish to refer to help(vglm) in the VGAM library.
Yee TW (2015). Vector Generalized Linear and Additive Models: With an Implementation in R. Springer, New York, USA.
Yee TW and Wild CJ (1996). “Vector Generalized Additive Models.” Journal of Royal Statistical Society, Series B, 58 (3), pp. 481-493.
Yee TW (2010). “The VGAM Package for Categorical Data Analysis.” Journal of Statistical Software, 32 (10), pp. 1-34. <URL: http://www.jstatsoft.org/v32/i10/>.
Yee TW and Hadi AF (2014). “Row-column interaction models, with an R implementation.” Computational Statistics, 29 (6), pp. 1427-1445.
Yee TW (2017). VGAM: Vector Generalized Linear and Additive Models. R package version 1.0-3, <URL: https://CRAN.R-project.org/package=VGAM>.
Yee TW (2013). “Two-parameter reduced-rank vector generalized linear models.” Computational Statistics and Data Analysis. <URL: http://ees.elsevier.com/csda>.
Yee TW, Stoklosa J and Huggins RM (2015). “The VGAM Package for Capture-Recapture Data Using the Conditional Likelihood.” Journal of Statistical Software, 65 (5), pp. 1-33. <URL: http://www.jstatsoft.org/v65/i05/>.