zelig-tobitbayes¶

Bayesian Tobit Regression

Bayesian tobit regression estimates a linear regression model with a censored dependent variable using a Gibbs sampler. The dependent variable may be censored from below and/or from above. For other linear regression models with fully observed dependent variables, see Bayesian regression, maximum likelihood normal regression, or least squares.

Syntax¶

With reference classes:

z5 <- ztobitbayes$new()
z5$zelig((Y ~ X1 + X2, below = 0, above = Inf, weights = w, data = mydata)
z5$setx()
z5$sim()

With the Zelig 4 compatibility wrappers:

z.out <- zelig(Y ~ X1 + X2, below = 0, above = Inf,
               model = "tobit.bayes", weights = w, data = mydata)
x.out <- setx(z.out)
s.out <- sim(z.out, x = x.out)

Inputs¶

zelig() accepts the following arguments to specify how the dependent variable is censored.

below: point at which the dependent variable is censored from below. If the dependent variable is only censored from above, set below = -Inf. The default value is 0.
above: point at which the dependent variable is censored from above. If the dependent variable is only censored from below, set above = Inf. The default value is Inf.

Additional Inputs¶

Use the following arguments to monitor the convergence of the Markov chain:

burnin: number of the initial MCMC iterations to be discarded (defaults to 1,000).
mcmc: number of the MCMC iterations after burnin (defaults to 10,000).
thin: thinning interval for the Markov chain. Only every thin-th draw from the Markov chain is kept. The value of mcmc must be divisible by this value. The default value is 1.
verbose: defaults to FALSE. If TRUE, the progress of the sampler (every ) is printed to the screen.
seed: seed for the random number generator. The default is NA which corresponds to a random seed of 12345.
beta.start: starting values for the Markov chain, either a scalar or vector with length equal to the number of estimated coefficients. The default is NA, such that the least squares estimates are used as the starting values.

Use the following parameters to specify the model’s priors:

b0: prior mean for the coefficients, either a numeric vector or a scalar. If a scalar, that value will be the prior mean for all coefficients. The default is 0.
B0: prior precision parameter for the coefficients, either a square matrix (with the dimensions equal to the number of the coefficients) or a scalar. If a scalar, that value times an identity matrix will be the prior precision parameter. The default is 0, which leads to an improper prior.
c0: c0/2 is the shape parameter for the Inverse Gamma prior on the variance of the disturbance terms.
d0: d0/2 is the scale parameter for the Inverse Gamma prior on the variance of the disturbance terms.

Zelig users may wish to refer to help(MCMCtobit) for more information.

Examples¶

Basic Example¶

Attaching the sample dataset:

data(tobin)

Estimating linear regression using tobit.bayes:

z.out <- zelig(durable ~ age + quant, model = "tobit.bayes",
               data = tobin, verbose = FALSE)

## Warning in readLines(zeligmixedmodels): incomplete final line found on
## '/usr/lib64/R/library/ZeligMultilevel/JSON/zelig5mixedmodels.json'

## How to cite this model in Zelig:
##   Ben Goodrich, and Ying Lu. 2013.
##   tobit-bayes: Bayesian Tobit Regression for a Censored Dependent Variable
##   in Christine Choirat, Christopher Gandrud, James Honaker, Kosuke Imai, Gary King, and Olivia Lau,
##   "Zelig: Everyone's Statistical Software," http://zeligproject.org/

You can check for convergence before summarizing the estimates with three diagnostic tests. See the section Diagnostics for Zelig Models for examples of the output with interpretation:

z.out$geweke.diag()
z.out$heidel.diag()
z.out$raftery.diag()

summary(z.out)

## Model:
##
## Iterations = 1001:11000
## Thinning interval = 1
## Number of chains = 1
## Sample size per chain = 10000
##
## 1. Empirical mean and standard deviation for each variable,
##    plus standard error of the mean:
##
##                 Mean      SD Naive SE Time-series SE
## (Intercept)  18.2488  41.224  0.41224        0.73852
## age          -0.2813   0.607  0.00607        0.01494
## quant        -0.0482   0.149  0.00149        0.00227
## sigma2      186.8462 433.981  4.33981       21.46249
##
## 2. Quantiles for each variable:
##
##                2.5%    25%     50%      75%   97.5%
## (Intercept) -59.154 -0.734 17.4816  35.8275 100.194
## age          -1.603 -0.502 -0.2151   0.0245   0.660
## quant        -0.336 -0.115 -0.0463   0.0189   0.229
## sigma2       19.608 49.165 88.5718 178.1512 917.721
##
## Next step: Use 'setx' method

Setting values for the explanatory variables to their sample averages:

x.out <- setx(z.out)

Simulating quantities of interest from the posterior distribution given x.out.

s.out1 <- sim(z.out, x = x.out)

summary(s.out1)

##
##  sim x :
##  -----
## ev
##   mean   sd  50%  2.5% 97.5%
## 1 2.09 1.45 1.75 0.598  5.69
## pv
##      mean   sd  50% 2.5% 97.5%
## [1,] 5.71 9.43 1.81    0    30

Simulating First Differences¶

Set explanatory variables to their default(mean/mode) values, with high (80th percentile) and low (20th percentile) liquidity ratio (quant):

x.high <- setx(z.out, quant = quantile(tobin$quant, prob = 0.8))
x.low <- setx(z.out, quant = quantile(tobin$quant, prob = 0.2))

Estimating the first difference for the effect of high versus low liquidity ratio on duration( durable):

s.out2 <- sim(z.out, x = x.high, x1 = x.low)

summary(s.out2)

##
##  sim x :
##  -----
## ev
##   mean   sd  50%  2.5% 97.5%
## 1 1.88 1.86 1.41 0.239  6.34
## pv
##      mean   sd  50% 2.5% 97.5%
## [1,] 5.62 9.71 1.56    0  30.4
##
##  sim x1 :
##  -----
## ev
##   mean   sd  50%  2.5% 97.5%
## 1 2.58 1.89 2.15 0.575  7.39
## pv
##      mean   sd  50% 2.5% 97.5%
## [1,] 5.96 9.34 2.28    0  30.4
## fd
##    mean   sd   50%  2.5% 97.5%
## 1 0.699 2.15 0.674 -3.38  4.88

Model¶

Let be the dependent variable which is not directly observed. Instead, we observe which is defined as following:

where is the lower bound below which is censored, and is the upper bound above which is censored.

The stochastic component is given by

where .
The systematic component is given by

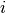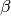where is the vector of explanatory variables for observation $i$ and $\beta$ is the vector of coefficients.
The semi-conjugate priors for 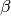$\beta$ and are given by

where is the vector of means for the explanatory variables, is the precision matrix (the inverse of a variance-covariance matrix), and and are the shape and scale parameters for . Note that 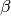$\beta$ and are assumed a priori independent.

Quantities of Interest¶

The expected values (qi$ev) for the tobit regression model is calculated as following. Let

where is the (cumulative) Normal density function and is the Normal probability density function of the standard normal distribution. Then the expected values are
The first difference (qi$fd) for the tobit regression model is defined as
In conditional prediction models, the average expected treatment effect (qi$att.ev) for the treatment group is

where is a binary explanatory variable defining the treatment () and control () groups.

Output Values¶

The Zelig object stores fields containing everything needed to rerun the Zelig output, and all the results and simulations as they are generated. In addition to the summary commands demonstrated above, some simply utility functions (known as getters) provide easy access to the raw fields most commonly of use for further investigation.

In the example above z.out$getcoef() returns the estimated coefficients, z.out$getvcov() returns the estimated covariance matrix, and z.out$getpredict() provides predicted values for all observations in the dataset from the analysis.