zelig-ls¶

Least Squares Regression for Continuous Dependent Variables

Use least squares regression analysis to estimate the best linear predictor for the specified dependent variables.

Syntax¶

With reference classes:

z5 <- zls$new()
z5$zelig(Y ~ X1 + X ~ X, weights = w, data = mydata)
z5$setx()
z5$sim()

With the Zelig 4 compatibility wrappers:

z.out <- zelig(Y ~ X1 + X2, model = "ls", weights = w, data = mydata)
x.out <- setx(z.out)
s.out <- sim(z.out, x = x.out)

Examples¶

Basic Example with First Differences¶

Attach sample data:

data(macro)

Estimate model:

z.out1 <- zelig(unem ~ gdp + capmob + trade, model = "ls", data = macro)

## Warning in readLines(zeligmixedmodels): incomplete final line found on
## '/usr/lib64/R/library/ZeligMultilevel/JSON/zelig5mixedmodels.json'

## How to cite this model in Zelig:
##   R Core Team. 2007.
##   ls: Least Squares Regression for Continuous Dependent Variables
##   in Christine Choirat, Christopher Gandrud, James Honaker, Kosuke Imai, Gary King, and Olivia Lau,
##   "Zelig: Everyone's Statistical Software," http://zeligproject.org/

Summarize regression coefficients:

summary(z.out1)

## Model:
##
## Call:
## z5$zelig(formula = unem ~ gdp + capmob + trade, data = macro)
##
## Residuals:
##    Min     1Q Median     3Q    Max
## -5.301 -2.077 -0.319  1.979  7.772
##
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)
## (Intercept)  6.18129    0.45057   13.72  < 2e-16
## gdp         -0.32360    0.06282   -5.15  4.4e-07
## capmob       1.42194    0.16644    8.54  4.2e-16
## trade        0.01985    0.00561    3.54  0.00045
##
## Residual standard error: 2.75 on 346 degrees of freedom
## Multiple R-squared:  0.288,      Adjusted R-squared:  0.282
## F-statistic: 46.6 on 3 and 346 DF,  p-value: <2e-16
##
## Next step: Use 'setx' method

Set explanatory variables to their default (mean/mode) values, with high (80th percentile) and low (20th percentile) values for the trade variable:

x.high <- setx(z.out1, trade = quantile(macro$trade, 0.8))
x.low <- setx(z.out1, trade = quantile(macro$trade, 0.2))

Generate first differences for the effect of high versus low trade on GDP:

s.out1 <- sim(z.out1, x = x.high, x1 = x.low)

summary(s.out1)

##
##  sim x :
##  -----
## ev
##   mean   sd  50% 2.5% 97.5%
## 1 5.43 0.19 5.44 5.05  5.81
## pv
##      mean   sd 50%  2.5% 97.5%
## [1,] 5.32 2.68 5.3 0.181  10.6
##
##  sim x1 :
##  -----
## ev
##   mean    sd 50% 2.5% 97.5%
## 1 4.59 0.181 4.6 4.23  4.94
## pv
##      mean   sd  50%   2.5% 97.5%
## [1,] 4.72 2.68 4.66 -0.384  10.1
## fd
##     mean    sd    50%  2.5%  97.5%
## 1 -0.838 0.229 -0.832 -1.29 -0.387

plot(s.out1)

Graphs of Quantities of Interest for Linear Regression

Using Dummy Variables¶

Estimate a model with fixed effects for each country (see for help with dummy variables). Note that you do not need to create dummy variables, as the program will automatically parse the unique values in the selected variable into discrete levels.

z.out2 <- zelig(unem ~ gdp + trade + capmob + as.factor(country), model = "ls", data = macro)

## Warning in readLines(zeligmixedmodels): incomplete final line found on
## '/usr/lib64/R/library/ZeligMultilevel/JSON/zelig5mixedmodels.json'

## How to cite this model in Zelig:
##   R Core Team. 2007.
##   ls: Least Squares Regression for Continuous Dependent Variables
##   in Christine Choirat, Christopher Gandrud, James Honaker, Kosuke Imai, Gary King, and Olivia Lau,
##   "Zelig: Everyone's Statistical Software," http://zeligproject.org/

Set values for the explanatory variables, using the default mean/mode values, with country set to the United States and Japan, respectively:

x.US <- setx(z.out2, country = "United States")
x.Japan <- setx(z.out2, country = "Japan")

Simulate quantities of interest:

s.out2 <- sim(z.out2, x = x.US, x1 = x.Japan)

plot(s.out2)

Graphs of Quantities of Interest for Linear Regression

Model¶

The stochastic component is described by a density with mean and the common variance
The systematic component models the conditional mean as

where is the vector of covariates, and 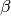$\beta$ is the vector of coefficients.

The least squares estimator is the best linear predictor of a dependent variable given , and minimizes the sum of squared residuals, .

Quantities of Interest¶

The expected value (qi$ev) is the mean of simulations from the stochastic component,

given a draw of 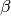$\beta$ from its sampling distribution.
In conditional prediction models, the average expected treatment effect (att.ev) for the treatment group is

where is a binary explanatory variable defining the treatment () and control () groups. Variation in the simulations are due to uncertainty in simulating , the counterfactual expected value of for observations in the treatment group, under the assumption that everything stays the same except that the treatment indicator is switched to .

Output Values¶

The output of each Zelig command contains useful information which you may view. For example, if you run z.out <- zelig(y ~ x, model = ls, data), then you may examine the available information in z.out by using names(z.out), see the coefficients by using z.out$coefficients, and a default summary of information through summary(z.out). Other elements available through the $ operator are listed below.

From the zelig() output object z.out, you may extract:
- coefficients: parameter estimates for the explanatory variables.
- residuals: the working residuals in the final iteration of the IWLS fit.
- fitted.values: fitted values.
- df.residual: the residual degrees of freedom.
- zelig.data: the input data frame if save.data = TRUE.
From summary(z.out), you may extract:
- coefficients: the parameter estimates with their associated standard errors, -values, and -statistics.
- sigma: the square root of the estimate variance of the random error :
- r.squared: the fraction of the variance explained by the model.
- adj.r.squared: the above statistic, penalizing for an increased number of explanatory variables.
- cov.unscaled: a matrix of unscaled covariances.