zelig-factorbayes¶

Bayesian Factor Analysis

Given some unobserved explanatory variables and observed dependent variables, the Normal theory factor analysis model estimates the latent factors. The model is implemented using a Markov Chain Monte Carlo algorithm (Gibbs sampling with data augmentation). For factor analysis with ordinal dependent variables, see ordered factor analysis (), and for a mix of types of dependent variables, see the mixed factor analysis model ().

Syntax¶

With reference classes:

z5 <- zfactorbayes$new()
z5$zelig(cbind(Y1 ,Y2, Y3) ~ NULL, factors = 2,
         model = "factor.bayes", weights = w, data = mydata)

With the Zelig 4 compatibility wrappers:

z.out <- zelig(cbind(Y1 ,Y2, Y3) ~ NULL, factors = 2,
               model = "factor.bayes", weights = w, data = mydata)

Inputs¶

zelig() takes the following functions for factor.bayes:

Y1, Y2, and Y3: variables of interest in factor analysis (manifest variables), assumed to be normally distributed. The model requires a minimum of three manifest variables.
factors: number of the factors to be fitted (defaults to 2).

Additional Inputs¶

In addition, zelig() accepts the following additional arguments for model specification:

lambda.constraints: list containing the equality or inequality constraints on the factor loadings. Choose from one of the following forms:
- varname = list(): by default, no constraints are imposed.
- varname = list(d, c): constrains the th loading for the variable named varname to be equal to c.
- varname = list(d, +): constrains the th loading for the variable named varname to be positive;
- varname = list(d, -): constrains the th loading for the variable named varname to be negative.
std.var: defaults to FALSE (manifest variables are rescaled to zero mean, but retain observed variance). If TRUE, the manifest variables are rescaled to be mean zero and unit variance.

In addition, zelig() accepts the following additional inputs for bayes.factor:

burnin: number of the initial MCMC iterations to be discarded (defaults to 1,000).
mcmc: number of the MCMC iterations after burnin (defaults to 20,000).
thin: thinning interval for the Markov chain. Only every thin-th draw from the Markov chain is kept. The value of mcmc must be divisible by this value. The default value is 1.
verbose: defaults to FALSE. If TRUE, the progress of the sampler (every ) is printed to the screen.
seed: seed for the random number generator. The default is NA which corresponds to a random seed 12345.
Lambda.start: starting values of the factor loading matrix , either a scalar (all unconstrained loadings are set to that value), or a matrix with compatible dimensions. The default is NA, where the start value are set to be 0 for unconstrained factor loadings, and 0.5 or 0.5 for constrained factor loadings (depending on the nature of the constraints).
Psi.start: starting values for the uniquenesses, either a scalar (the starting values for all diagonal elements of are set to be this value), or a vector with length equal to the number of manifest variables. In the latter case, the starting values of the diagonal elements of take the values of Psi.start. The default value is NA where the starting values of the all the uniquenesses are set to be 0.5.
store.lambda: defaults to TRUE, which stores the posterior draws of the factor loadings.
store.scores: defaults to FALSE. If TRUE, stores the posterior draws of the factor scores. (Storing factor scores may take large amount of memory for a large number of draws or observations.)

The model also accepts the following additional arguments to specify prior parameters:

l0: mean of the Normal prior for the factor loadings, either a scalar or a matrix with the same dimensions as . If a scalar value, that value will be the prior mean for all the factor loadings. Defaults to 0.
L0: precision parameter of the Normal prior for the factor loadings, either a scalar or a matrix with the same dimensions as . If L0 takes a scalar value, then the precision matrix will be a diagonal matrix with the diagonal elements set to that value. The default value is 0, which leads to an improper prior.
a0: the shape parameter of the Inverse Gamma prior for the uniquenesses is a0/2. It can take a scalar value or a vector. The default value is 0.001.
b0: the scale parameter of the Inverse Gamma prior for the uniquenesses is b0/2. It can take a scalar value or a vector. The default value is 0.001.

Zelig users may wish to refer to help(MCMCfactanal) for more information.

Example¶

Attaching the sample dataset:

data(swiss)
names(swiss) <- c("Fert", "Agr", "Exam", "Educ", "Cath", "InfMort")

Factor analysis:

z.out <- zelig(~ Agr + Exam + Educ + Cath + InfMort,
               model = "factor.bayes", data = swiss,
               factors = 2, verbose = FALSE,
               a0 = 1, b0 = 0.15, burnin = 500, mcmc = 5000)

## Warning in readLines(zeligmixedmodels): incomplete final line found on
## '/usr/lib64/R/library/ZeligMultilevel/JSON/zelig5mixedmodels.json'

## How to cite this model in Zelig:
##   Andrew D. Martin, Kevin M. Quinn, and Jong Hee Park. 2013.
##   factor-bayes: Bayesian Factor Analysis
##   in Christine Choirat, Christopher Gandrud, James Honaker, Kosuke Imai, Gary King, and Olivia Lau,
##   "Zelig: Everyone's Statistical Software," http://zeligproject.org/

Checking for convergence before summarizing the estimates. See the section Diagnostics for Zelig Models for examples of the output with interpretation:

z.out$geweke.diag()

##
## Fraction in 1st window = 0.1
## Fraction in 2nd window = 0.5
##
##     LambdaAgr_1     LambdaAgr_2    LambdaExam_1    LambdaExam_2
##         -2.5274         -0.4865          2.2733          1.1564
##    LambdaEduc_1    LambdaEduc_2    LambdaCath_1    LambdaCath_2
##          3.4297         -0.4123         -0.7767         -4.0678
## LambdaInfMort_1 LambdaInfMort_2          PsiAgr         PsiExam
##         -1.9580         -6.3315          0.4583         -0.8415
##         PsiEduc         PsiCath      PsiInfMort
##          0.3491          0.2581          0.5271

Since the algorithm did not converge, we now add some constraints on to optimize the algorithm:

z.out <- zelig(~ Agr + Exam + Educ + Cath + InfMort,
               model = "factor.bayes", data = swiss, factors = 2,
               lambda.constraints =
                   list(Exam = list(1,"+"),
                        Exam = list(2,"-"),
                        Educ = c(2, 0),
                        InfMort = c(1, 0)),
               verbose = FALSE, a0 = 1, b0 = 0.15,
               burnin = 500, mcmc = 5000)

## Warning in readLines(zeligmixedmodels): incomplete final line found on
## '/usr/lib64/R/library/ZeligMultilevel/JSON/zelig5mixedmodels.json'

## How to cite this model in Zelig:
##   Andrew D. Martin, Kevin M. Quinn, and Jong Hee Park. 2013.
##   factor-bayes: Bayesian Factor Analysis
##   in Christine Choirat, Christopher Gandrud, James Honaker, Kosuke Imai, Gary King, and Olivia Lau,
##   "Zelig: Everyone's Statistical Software," http://zeligproject.org/

z.out$geweke.diag()

##
## Fraction in 1st window = 0.1
## Fraction in 2nd window = 0.5
##
##     LambdaAgr_1     LambdaAgr_2    LambdaExam_1    LambdaExam_2
##         0.18321        -0.31899        -0.62450         0.93821
##    LambdaEduc_1    LambdaCath_1    LambdaCath_2 LambdaInfMort_2
##        -1.74708        -0.01196         0.88088         1.66103
##          PsiAgr         PsiExam         PsiEduc         PsiCath
##        -1.42872         1.21346         0.73458        -0.70383
##      PsiInfMort
##         0.24604

z.out$heidel.diag()

##
##                 Stationarity start     p-value
##                 test         iteration
## LambdaAgr_1     passed        1        0.404
## LambdaAgr_2     passed        1        0.476
## LambdaExam_1    passed        1        0.854
## LambdaExam_2    passed        1        0.485
## LambdaEduc_1    passed        1        0.534
## LambdaCath_1    passed        1        0.887
## LambdaCath_2    passed        1        0.770
## LambdaInfMort_2 failed       NA        0.021
## PsiAgr          passed        1        0.289
## PsiExam         passed        1        0.828
## PsiEduc         passed        1        0.301
## PsiCath         passed        1        0.649
## PsiInfMort      passed        1        0.414
##
##                 Halfwidth Mean   Halfwidth
##                 test
## LambdaAgr_1     passed    -0.737 0.01479
## LambdaAgr_2     passed     0.306 0.01497
## LambdaExam_1    passed     0.816 0.02123
## LambdaExam_2    passed    -0.520 0.01469
## LambdaEduc_1    passed     0.949 0.01675
## LambdaCath_1    failed    -0.195 0.02311
## LambdaCath_2    passed     0.917 0.02333
## LambdaInfMort_2 <NA>          NA      NA
## PsiAgr          passed     0.443 0.00589
## PsiExam         passed     0.163 0.00943
## PsiEduc         passed     0.199 0.01552
## PsiCath         failed     0.209 0.02745
## PsiInfMort      passed     0.996 0.00651

z.out$raftery.diag()

##
## Quantile (q) = 0.025
## Accuracy (r) = +/- 0.005
## Probability (s) = 0.95
##
##                  Burn-in  Total Lower bound  Dependence
##                  (M)      (N)   (Nmin)       factor (I)
##  LambdaAgr_1     15       14712 3746         3.93
##  LambdaAgr_2     30       28143 3746         7.51
##  LambdaExam_1    10       11258 3746         3.01
##  LambdaExam_2    10       13332 3746         3.56
##  LambdaEduc_1    8        10468 3746         2.79
##  LambdaCath_1    44       37220 3746         9.94
##  LambdaCath_2    32       32548 3746         8.69
##  LambdaInfMort_2 3        4198  3746         1.12
##  PsiAgr          8        10020 3746         2.67
##  PsiExam         24       23420 3746         6.25
##  PsiEduc         24       22720 3746         6.07
##  PsiCath         19       20303 3746         5.42
##  PsiInfMort      3        4198  3746         1.12

summary(z.out)

## Model:
##
## Iterations = 501:5500
## Thinning interval = 1
## Number of chains = 1
## Sample size per chain = 5000
##
## 1. Empirical mean and standard deviation for each variable,
##    plus standard error of the mean:
##
##                    Mean      SD Naive SE Time-series SE
## LambdaAgr_1     -0.7366 0.15317 0.002166       0.007545
## LambdaAgr_2      0.3055 0.14996 0.002121       0.007636
## LambdaExam_1     0.8158 0.15116 0.002138       0.010832
## LambdaExam_2    -0.5197 0.12488 0.001766       0.007492
## LambdaEduc_1     0.9485 0.14205 0.002009       0.008546
## LambdaCath_1    -0.1954 0.17714 0.002505       0.011793
## LambdaCath_2     0.9172 0.16608 0.002349       0.011904
## LambdaInfMort_2  0.1660 0.17111 0.002420       0.004198
## PsiAgr           0.4434 0.11534 0.001631       0.003004
## PsiExam          0.1626 0.07754 0.001097       0.004813
## PsiEduc          0.1989 0.11758 0.001663       0.007919
## PsiCath          0.2087 0.16319 0.002308       0.014003
## PsiInfMort       0.9962 0.22195 0.003139       0.003319
##
## 2. Quantiles for each variable:
##
##                      2.5%      25%     50%     75%   97.5%
## LambdaAgr_1     -1.051946 -0.83226 -0.7313 -0.6346 -0.4483
## LambdaAgr_2     -0.002689  0.21719  0.3081  0.4019  0.5888
## LambdaExam_1     0.539739  0.70957  0.8096  0.9138  1.1320
## LambdaExam_2    -0.757806 -0.60299 -0.5184 -0.4394 -0.2779
## LambdaEduc_1     0.689616  0.85378  0.9383  1.0298  1.2579
## LambdaCath_1    -0.559656 -0.31029 -0.1903 -0.0751  0.1338
## LambdaCath_2     0.560127  0.82241  0.9267  1.0197  1.2260
## LambdaInfMort_2 -0.170265  0.05400  0.1639  0.2751  0.5135
## PsiAgr           0.256945  0.36232  0.4308  0.5098  0.7011
## PsiExam          0.038478  0.10442  0.1547  0.2117  0.3334
## PsiEduc          0.033024  0.11025  0.1819  0.2702  0.4671
## PsiCath          0.026496  0.08401  0.1578  0.3005  0.6203
## PsiInfMort       0.649015  0.83760  0.9645  1.1209  1.5143
##
## Next step: Use 'setx' method

Model¶

Suppose for observation 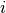$i$ we observe variables and hypothesize that there are underlying factors such that:

where is the vector of manifest variables for observation 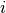$i$ . is the factor loading matrix and is the -vector of latent factor scores. Both and need to be estimated.

The stochastic component is given by:

where is a diagonal, positive definite matrix. The diagonal elements of are referred to as uniquenesses.
The systematic component is given by
The independent conjugate prior for each is given by
The independent conjugate prior for each is given by
The prior for is

where is a :math:` dtimes d ` identity matrix.

Output Values¶

The output of each Zelig command contains useful information which you may view. For example, if you run:

z.out <- zelig(cbind(Y1, Y2, Y3), model = "factor.bayes", data)

then you may examine the available information in z.out by using names(z.out), see the draws from the posterior distribution of the coefficients by using z.out$coefficients, and view a default summary of information through summary(z.out). Other elements available through the $ operator are listed below.

From the zelig() output object z.out, you may extract:
- coefficients: draws from the posterior distributions of the estimated factor loadings and the uniquenesses. If store.scores = TRUE, the estimated factors scores are also contained in coefficients.
- data: the name of the input data frame.
- seed: the random seed used in the model.
Since there are no explanatory variables, the sim() procedure is not applicable for factor analysis models.