zeligchoice-oprobit¶
Ordinal Probit Regression for Ordered Categorical Dependent Variables
Use the ordinal probit regression model if your dependent variables are ordered and categorical. They may take on either integer values or character strings. For a Bayesian implementation of this model, see oprobitbayes.
Syntax¶
First load packages:
library("Zelig")
library("ZeligChoice")
With reference classes:
z5 <- zoprobit$new()
z5$zelig(as.factor(Y) ~ X1 + X2, data = mydata)
z5$setx()
z5$sim()
With the Zelig 4 compatibility wrappers:
z.out <- zelig(as.factor(Y) ~ X1 + X23,
model = "oprobit", data = mydata)
x.out <- setx(z.out)
s.out <- sim(z.out, x = x.out, x1 = NULL)
If Y takes discrete integer values, the as.factor() command will order it automatically. If Y takes on values composed of character strings, such as “strongly agree”, “agree”, and “disagree”, as.factor() will order the values in the order in which they appear in Y. You will need to replace your dependent variable with a factored variable prior to estimating the model through zelig(). See for more information on creating ordered factors and Example below.
Example¶
Creating An Ordered Dependent Variable¶
Load the sample data:
data(sanction)
Create an ordered dependent variable:
sanction$ncost <- factor(sanction$ncost, ordered = TRUE,
levels = c("net gain", "little effect", "modest lost", "major loss"))
Estimate the model:
z.out <- zelig(ncost ~ mil + coop, model = "oprobit", data = sanction)
## Warning in readLines(zeligmixedmodels): incomplete final line found on
## '/usr/lib64/R/library/ZeligMultilevel/JSON/zelig5mixedmodels.json'
## How to cite this model in Zelig:
## William N. Venables, and Brian D. Ripley. 2011.
## oprobit: Ordinal Probit Regression for Ordered Categorical Dependent Variables
## in Christine Choirat, Christopher Gandrud, James Honaker, Kosuke Imai, Gary King, and Olivia Lau,
## "Zelig: Everyone's Statistical Software," http://zeligproject.org/
Summarize estimated paramters:
summary(z.out)
## Model:
## Call:
## z5$zelig(formula = ncost ~ mil + coop, data = sanction)
##
## Coefficients:
## Value Std. Error t value
## mil 0.275 0.466 0.589
## coop 0.494 0.172 2.870
##
## Intercepts:
## Value Std. Error t value
## net gain|little effect 0.669 0.309 2.166
## little effect|modest lost 2.798 0.476 5.872
## modest lost|major loss 2.798 0.476 5.872
##
## Residual Deviance: 104.90
## AIC: 114.90
## (9 observations deleted due to missingness)
## Next step: Use 'setx' method
Set the explanatory variables to their observed values:
x.out <- setx(z.out)
Simulate fitted values given x.out and view the results:
s.out <- sim(z.out, x = x.out)
summary(s.out)
##
## sim x :
## -----
## ev
## mean sd 50% 2.5% 97.5%
## net gain 4.20e-01 6.15e-02 4.21e-01 3.06e-01 5.44e-01
## little effect 5.22e-01 8.98e-02 5.27e-01 3.14e-01 6.73e-01
## modest lost 1.45e-05 1.17e-05 1.28e-05 3.25e-10 3.55e-05
## major loss 5.74e-02 7.66e-02 2.47e-02 1.07e-07 2.68e-01
## pv
## mean sd 50% 2.5% 97.5%
## [1,] 1.7 0.71 2 1 4
plot(s.out)
Graphs of Quantities of Interest for Ordered Probit
First Differences¶
Using the sample data sanction, let us estimate the empirical model and return the coefficients:
z.out <- zelig(as.factor(cost) ~ mil + coop, model = "oprobit",
data = sanction)
## Warning in readLines(zeligmixedmodels): incomplete final line found on
## '/usr/lib64/R/library/ZeligMultilevel/JSON/zelig5mixedmodels.json'
## How to cite this model in Zelig:
## William N. Venables, and Brian D. Ripley. 2011.
## oprobit: Ordinal Probit Regression for Ordered Categorical Dependent Variables
## in Christine Choirat, Christopher Gandrud, James Honaker, Kosuke Imai, Gary King, and Olivia Lau,
## "Zelig: Everyone's Statistical Software," http://zeligproject.org/
summary(z.out)
## Model:
## Call:
## z5$zelig(formula = as.factor(cost) ~ mil + coop, data = sanction)
##
## Coefficients:
## Value Std. Error t value
## mil -0.0353 0.430 -0.0822
## coop 0.5871 0.145 4.0558
##
## Intercepts:
## Value Std. Error t value
## 1|2 0.698 0.280 2.492
## 2|3 2.250 0.363 6.190
## 3|4 3.108 0.440 7.066
##
## Residual Deviance: 153.54
## AIC: 163.54
## Next step: Use 'setx' method
Set the explanatory variables to their means, with coop set to 1 (the lowest value) in the baseline case and set to 4 (the highest value) in the alternative case:
x.low <- setx(z.out, coop = 1)
x.high <- setx(z.out, coop = 4)
Generate simulated fitted values and first differences, and view the results:
s.out2 <- sim(z.out, x = x.low, x1 = x.high)
summary(s.out2)
##
## sim x :
## -----
## ev
## mean sd 50% 2.5% 97.5%
## 1 0.5429 0.0700 0.54459 4.06e-01 0.676
## 2 0.3853 0.0549 0.38746 2.75e-01 0.491
## 3 0.0491 0.0398 0.03969 6.69e-04 0.135
## 4 0.0227 0.0395 0.00532 1.82e-07 0.140
## pv
## mean sd 50% 2.5% 97.5%
## [1,] 1.6 0.729 1 1 4
##
## sim x1 :
## -----
## ev
## mean sd 50% 2.5% 97.5%
## 1 0.0596 0.0423 0.0507 0.00940 0.164
## 2 0.4312 0.1597 0.4115 0.18618 0.797
## 3 0.2807 0.0886 0.2782 0.12553 0.454
## 4 0.2285 0.1601 0.2057 0.00312 0.567
## pv
## mean sd 50% 2.5% 97.5%
## [1,] 2.72 0.885 3 1 4
## fd
## mean sd 50% 2.5% 97.5%
## 1 -0.4833 0.0847 -0.4878 -0.63718 -0.302
## 2 0.0458 0.1577 0.0202 -0.19773 0.411
## 3 0.2317 0.1038 0.2351 0.03671 0.428
## 4 0.2058 0.1345 0.1957 0.00312 0.472
plot(s.out2)
Graphs of Quantities of Interest for Ordered Probit
Model¶
Let be the ordered categorical dependent variable for
observation 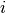 that takes one of the integer values from
to where is the total number of
categories.
that takes one of the integer values from
to where is the total number of
categories.
The stochastic component is described by an unobserved continuous variable, , which follows the normal distribution with mean and unit variance
The observation mechanism is
where for is the threshold parameter with the following constraints; for all and and .
Given this observation mechanism, the probability for each category, is given by
where is the cumulative distribution function for the Normal distribution with mean and unit variance.
The systematic component is given by
where is the vector of explanatory variables and
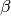 is the vector of coefficients.
is the vector of coefficients.
Quantities of Interest¶
The expected values (qi$ev) for the ordinal probit model are simulations of the predicted probabilities for each category:
given draws of
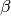 from its posterior.
from its posterior.The predicted value (qi$pr) is the observed value of given the underlying standard normal distribution described by .
The difference in each of the predicted probabilities (qi$fd) is given by
In conditional prediction models, the average expected treatment effect (qi$att.ev) for the treatment group in category is
where is a binary explanatory variable defining the treatment () and control () groups, and is the number of treated observations in category .
In conditional prediction models, the average predicted treatment effect (qi$att.pr) for the treatment group in category is
where is a binary explanatory variable defining the treatment () and control () groups, and is the number of treated observations in category .
Output Values¶
The output of each Zelig command contains useful information which you may view. For example, if you run z.out <- zelig(y ~ x, model = oprobit, data), then you may examine the available information in z.out by using names(z.out), see the coefficients by using z.out$coefficients, and a default summary of information through summary(z.out). Other elements available through the $ operator are listed below.
- From the zelig() output object z.out, you may extract:
- coefficients: the named vector of coefficients.
- fitted.values: an matrix of the in-sample fitted values.
- predictors: an matrix of the linear predictors .
- residuals: an matrix of the residuals.
- zeta: a vector containing the estimated class boundaries.
- df.residual: the residual degrees of freedom.
- df.total: the total degrees of freedom.
- rss: the residual sum of squares.
- y: an matrix of the dependent variables.
- zelig.data: the input data frame if save.data = TRUE.
- From summary(z.out), you may extract:
- coef3: a table of the coefficients with their associated standard errors and -statistics.
- cov.unscaled: the variance-covariance matrix.
- pearson.resid: an matrix of the Pearson residuals.
See also¶
The ordinal probit function is part of the VGAM package by Thomas Yee. In addition, advanced users may wish to refer to help(vglm) in the VGAM library.
Venables WN and Ripley BD (2002). Modern Applied Statistics with S, Fourth edition. Springer, New York. ISBN 0-387-95457-0, <URL: http://www.stats.ox.ac.uk/pub/MASS4>.