zeliggam-normalgam¶

Syntax¶

With reference classes:

z5 <- znormalgam$new()
z5$zelig(y ~ x1 + s(x2), data = mydata)
z5$setx()
z5$sim()

With the Zelig 4 compatibility wrappers:

z.out <- zelig(y ~ x1 + s(x2), model = "normal.gam", data = mydata)
x.out <- setx(z.out)
s.out <- sim(z.out, x = x.out)

where s() indicates a variable to be estimated via nonparametric smooth. All variables for which s() is not specified, are estimated via standard parametric methods.

Additional Inputs¶

In addition to the standard inputs, zelig() takes the following additional options for GAM models.

• method: Controls the fitting method to be used. Fitting

  methods are selected via a list environment within method = gam.method(). See gam.method() for details.

• scale: Generalized Cross Validation (GCV) is used if

  scale = 0 (see the “Model” section for details) except for Logit models where a Un-Biased Risk Estimator (UBRE) (also see the “Model” section for details) is used with a scale parameter assumed to be 1. If scale is greater than 1, it is assumed to be the scale parameter/variance and UBRE is used. If scale is negative GCV is used.

• knots: An optional list of knot values to be used for the construction of basis functions.

• H: A user supplied fixed quadratic penalty on the parameters of the GAM can be supplied with this as its coefficient matrix. For example, ridge penalties can be added to the parameters of the GAM to aid in identification on the scale of the linear predictor.

• sp: A vector of smoothing parameters for each term.

• ...: additional options passed to the normal.gam model. See the mgcv library for details.

Examples¶

rm(list=ls(pattern="\\.out"))
suppressWarnings(suppressMessages(library(ZeligGAM)))
set.seed(1234)

set.seed(0)
n <- 400
sig <- 2
x0 <- runif(n, 0, 1)
x1 <- runif(n, 0, 1)
x2 <- runif(n, 0, 1)
x3 <- runif(n, 0, 1)
f0 <- function(x) 2 * sin(pi * x)
f1 <- function(x) exp(2 * x)
f2 <-  function(x) 0.2 * x^11 * (10 * (1 - x))^6 + 10 * (10 * x)^3 * (1 - x)^10
f3 <- function(x) 0 * x
f <- f0(x0) + f1(x1) + f2(x2)
e <- rnorm(n, 0, sig)
y <- f + e
my.data <- as.data.frame(cbind(y, x0, x1, x2, x3))

z.out <- zelig(y ~ s(x0) + s(x1) + s(x2) + s(x3), model = "normal.gam", data = my.data)

## How to cite this model in Zelig:
##   Christine Choirat, James Honaker, Kosuke Imai, Gary King, and Olivia Lau. 2011.
##   normal-gam: Generalized Additive Model for Normal Regression of Continuous Dependent Variables
##   in Christine Choirat, James Honaker, Kosuke Imai, Gary King, and Olivia Lau,
##   "Zelig: Everyone's Statistical Software," http://zeligproject.org/

summary(z.out)

## Model:
##
## Family: gaussian
## Link function: identity
##
## Formula:
## y ~ s(x0) + s(x1) + s(x2) + s(x3)
##
## Parametric coefficients:
##             Estimate Std. Error t value Pr(>|t|)
## (Intercept)    7.915      0.105    75.4   <2e-16
##
## Approximate significance of smooth terms:
##        edf Ref.df      F p-value
## s(x0) 5.17   6.29   4.56 0.00013
## s(x1) 2.36   2.93 103.05 < 2e-16
## s(x2) 8.52   8.93  84.31 < 2e-16
## s(x3) 1.00   1.00   0.44 0.50693
##
## R-sq.(adj) =  0.726   Deviance explained = 73.7%
## GCV =  4.611  Scale est. = 4.4029    n = 400
## Next step: Use 'setx' method

plot(z.out$zelig.out$z.out[[1]], pages = 1, residuals = TRUE)

z.out <- zelig(y ~ s(x0) + s(x1) + s(x2) + s(x3), model = "normal.gam", data = my.data)

## How to cite this model in Zelig:
##   Christine Choirat, James Honaker, Kosuke Imai, Gary King, and Olivia Lau. 2011.
##   normal-gam: Generalized Additive Model for Normal Regression of Continuous Dependent Variables
##   in Christine Choirat, James Honaker, Kosuke Imai, Gary King, and Olivia Lau,
##   "Zelig: Everyone's Statistical Software," http://zeligproject.org/

summary(z.out)

## Model:
##
## Family: gaussian
## Link function: identity
##
## Formula:
## y ~ s(x0) + s(x1) + s(x2) + s(x3)
##
## Parametric coefficients:
##             Estimate Std. Error t value Pr(>|t|)
## (Intercept)    7.915      0.105    75.4   <2e-16
##
## Approximate significance of smooth terms:
##        edf Ref.df      F p-value
## s(x0) 5.17   6.29   4.56 0.00013
## s(x1) 2.36   2.93 103.05 < 2e-16
## s(x2) 8.52   8.93  84.31 < 2e-16
## s(x3) 1.00   1.00   0.44 0.50693
##
## R-sq.(adj) =  0.726   Deviance explained = 73.7%
## GCV =  4.611  Scale est. = 4.4029    n = 400
## Next step: Use 'setx' method

plot(s.out)

## Error in plot(s.out): object 's.out' not found

x.high <- setx(z.out, x3 = quantile(my.data$x3, 0.8))
x.low <- setx(z.out, x3 = quantile(my.data$x3, 0.2))
s.out <- sim(z.out, x = x.high, x1 = x.low)
summary(s.out)

##
##  sim x :
##  -----
## ev
##      mean    sd  50% 2.5% 97.5%
## [1,]  7.9 0.418 7.89  7.1  8.71
## pv
##      mean    sd  50% 2.5% 97.5%
## [1,] 7.93 0.376 7.93 7.16  8.65
##
##  sim x1 :
##  -----
## ev
##      mean    sd  50% 2.5% 97.5%
## [1,] 8.05 0.391 8.05 7.26  8.78
## pv
##      mean    sd  50% 2.5% 97.5%
## [1,] 8.06 0.408 8.06 7.26  8.86
## fd
##       mean    sd   50%  2.5% 97.5%
## [1,] 0.151 0.582 0.158 -1.08   1.2

plot(s.out)

x.high <- setx(z.out, x3 = quantile(my.data$x3, 0.8))
x.low <- setx(z.out, x3 = quantile(my.data$x3, 0.2))
s.out <- sim(z.out, x = x.high, x1 = x.low)
summary(s.out)

##
##  sim x :
##  -----
## ev
##      mean    sd  50% 2.5% 97.5%
## [1,] 7.91 0.398 7.92 7.12  8.68
## pv
##      mean    sd  50% 2.5% 97.5%
## [1,] 7.91 0.389 7.91 7.17  8.66
##
##  sim x1 :
##  -----
## ev
##      mean    sd  50% 2.5% 97.5%
## [1,] 8.06 0.396 8.07  7.3  8.85
## pv
##      mean    sd  50% 2.5% 97.5%
## [1,] 8.05 0.403 8.05 7.28  8.82
## fd
##       mean    sd   50%   2.5% 97.5%
## [1,] 0.156 0.567 0.136 -0.948  1.35

plot(z.out$zelig.out$z.out[[1]], pages = 1, residuals = TRUE)

z.out <- zelig(y ~ s(x0) + s(x1) + s(x2) + s(x3), sp = c(0.01, -1, -1, -1), model = "normal.gam", data = my.data)

## How to cite this model in Zelig:
##   Christine Choirat, James Honaker, Kosuke Imai, Gary King, and Olivia Lau. 2011.
##   normal-gam: Generalized Additive Model for Normal Regression of Continuous Dependent Variables
##   in Christine Choirat, James Honaker, Kosuke Imai, Gary King, and Olivia Lau,
##   "Zelig: Everyone's Statistical Software," http://zeligproject.org/

summary(z.out)

## Model:
##
## Family: gaussian
## Link function: identity
##
## Formula:
## y ~ s(x0) + s(x1) + s(x2) + s(x3)
##
## Parametric coefficients:
##             Estimate Std. Error t value Pr(>|t|)
## (Intercept)    7.915      0.105    75.4   <2e-16
##
## Approximate significance of smooth terms:
##        edf Ref.df      F p-value
## s(x0) 7.98   8.72   3.79 0.00017
## s(x1) 2.35   2.92 102.12 < 2e-16
## s(x2) 8.51   8.93  83.58 < 2e-16
## s(x3) 1.00   1.00   0.62 0.43251
##
## R-sq.(adj) =  0.726   Deviance explained = 73.9%
## GCV = 4.6472  Scale est. = 4.4052    n = 400
## Next step: Use 'setx' method

plot(z.out$zelig.out$z.out[[1]], pages = 1, residuals = TRUE)

z.out <- zelig(y ~ s(x0) + s(x1) + s(x2) + s(x3), min.sp = c(0.001, + 0.01, 0, 10), model = "normal.gam", data = my.data)

## How to cite this model in Zelig:
##   Christine Choirat, James Honaker, Kosuke Imai, Gary King, and Olivia Lau. 2011.
##   normal-gam: Generalized Additive Model for Normal Regression of Continuous Dependent Variables
##   in Christine Choirat, James Honaker, Kosuke Imai, Gary King, and Olivia Lau,
##   "Zelig: Everyone's Statistical Software," http://zeligproject.org/

summary(z.out)

## Model:
##
## Family: gaussian
## Link function: identity
##
## Formula:
## y ~ s(x0) + s(x1) + s(x2) + s(x3)
##
## Parametric coefficients:
##             Estimate Std. Error t value Pr(>|t|)
## (Intercept)    7.915      0.105    75.4   <2e-16
##
## Approximate significance of smooth terms:
##        edf Ref.df      F p-value
## s(x0) 5.17   6.29   4.56 0.00013
## s(x1) 2.36   2.93 103.05 < 2e-16
## s(x2) 8.52   8.93  84.31 < 2e-16
## s(x3) 1.00   1.00   0.44 0.50693
##
## R-sq.(adj) =  0.726   Deviance explained = 73.7%
## GCV =  4.611  Scale est. = 4.4029    n = 400
## Next step: Use 'setx' method

plot(z.out$zelig.out$z.out[[1]], pages = 1)

z.out <- zelig(y ~ s(x0, k = 4, fx = TRUE, bs = "tp") + s(x1, k = 12) + s(x2, k = 15), model = "normal.gam", data = my.data)

## How to cite this model in Zelig:
##   Christine Choirat, James Honaker, Kosuke Imai, Gary King, and Olivia Lau. 2011.
##   normal-gam: Generalized Additive Model for Normal Regression of Continuous Dependent Variables
##   in Christine Choirat, James Honaker, Kosuke Imai, Gary King, and Olivia Lau,
##   "Zelig: Everyone's Statistical Software," http://zeligproject.org/

summary(z.out)

## Model:
##
## Family: gaussian
## Link function: identity
##
## Formula:
## y ~ s(x0, k = 4, fx = TRUE, bs = "tp") + s(x1, k = 12) + s(x2,
##     k = 15)
##
## Parametric coefficients:
##             Estimate Std. Error t value Pr(>|t|)
## (Intercept)    7.915      0.105    75.6   <2e-16
##
## Approximate significance of smooth terms:
##         edf Ref.df      F p-value
## s(x0)  3.00   3.00   8.37 2.1e-05
## s(x1)  2.38   2.96 101.57 < 2e-16
## s(x2) 11.74  13.18  57.90 < 2e-16
##
## R-sq.(adj) =  0.727   Deviance explained = 73.8%
## GCV = 4.5965  Scale est. = 4.3882    n = 400
## Next step: Use 'setx' method

plot(z.out$zelig.out$z.out[[1]], pages = 1)

The Model¶

GAM models use families the same way GLM models do: they specify the distribution and link function to use in model fitting. In the case of normal.gam a normal link function is used. Specifically, let be the continuous dependent variable for observation .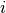

• The stochastic component is described by a univariate normal model

  with a vector of means and scalar variance :

• The systematic component is given by:

  where is the vector of explanatory variables, is

  the vector of coefficients and for is the set of smooth terms.

Generalized additive models (GAMs) are similar in many respects to generalized linear models (GLMs). Specifically, GAMs are generally fit by penalized maximum likelihood estimation and GAMs have (or can have) a parametric component identical to that of a GLM. The difference is that GAMs also include in their linear predictors a specified sum of smooth functions.

In this GAM implementation, smooth functions are represented using penalized regression splines. Two techniques may be used to estimate smoothing parameters: Generalized Cross Validation (GCV),

or an Un-Biased Risk Estimator (UBRE) (which is effectively just a rescaled AIC),

where is the deviance, is the number of observations, is the scale parameter, and is the effective degrees of freedom of the model. The use of GCV or UBRE can be set by the user with the scale command described in the “Additional Inputs” section and in either case, smoothing parameters are chosen to minimize the GCV or UBRE score for the model.

Estimation for GAM models proceeds as follows: first, basis functions and a set (one or more) of quadratic penalty coefficient matrices are constructed for each smooth term. Second, a model matrix is obtained for the parametric component of the GAM. These matrices are combined to produce a complete model matrix and a set of penalty matrices for the smooth terms. Iteratively Reweighted Least Squares (IRLS) is then used to estimate the model; at each iteration of the IRLS, a penalized weighted least squares model is run and the smoothing parameters of that model are estimated by GCV or UBRE. This process is repeated until convergence is achieved.

Further details of the GAM fitting process are given in Wood (2000, 2004, 2006).

Quantities of Interest¶

The quantities of interest for the normal.gam model are the same as those for the standard logistic regression.

• The expected value (qi$ev) for the normal.gam model is the mean of simulations from the stochastic component,

• The predicted values (qi$pr) are draws from the Normal distribution defined by the set of parameters .

• The first difference (qi$fd) for the normal.gam model is defined as

  for .

Output Values¶

The output of each Zelig command contains useful information which you may view. For example, if you run z.out <- zelig(y ~ x, model = "normal.gam", data), then you may examine the available information in z.out by using names(z.out), see the coefficients by using coefficients(z.out), and a default summary of information through summary(z.out). Other elements available through the $ operator are listed below.

• From the zelig() output stored in z.out$zelig.out$z.out[[1]], you may extract:
  • coefficients: parameter estimates for the explanatory variables.
  • fitted.values: the vector of fitted values for the explanatory variables.
  • residuals: the working residuals in the final iteration of the IRLS fit.
  • linear.predictors: the vector of .
  • aic: Akaike’s Information Criterion (minus twice the maximized log-likelihood plus twice the number of coefficients).
  • method: the fitting method used.
  • converged: logical indicating weather the model converged or not.
  • smooth: information about the smoothed parameters.
  • df.residual: the residual degrees of freedom.
  • df.null: the residual degrees of freedom for the null model.
  • data: the input data frame.
  • model: the model matrix used.
• From summary(z.out), you may extract:
  • p.coeff: the coefficients of the parametric components of the model.
  • se: the standard errors of the entire model.
  • p.table: the coefficients, standard errors, and associated statistics for the parametric portion of the model.
  • s.table: the table of estimated degrees of freedom, estimated rank, statistics, and values for the nonparametric portion of the model.
  • cov.scaled: a matrix of scaled covariances.
  • cov.unscaled: a matrix of unscaled covariances.
• From the sim() output stored in s.out, you may extract:
  • qi$ev: the simulated expected probabilities for the specified values of x.
  • qi$pr: the simulated predicted values for the specified values of x.
  • qi$fd: the simulated first differences in the expected probabilities simulated from x and x1.

See also¶

The normal.gam model is adapted from the mgcv package by Simon N. Wood. Advanced users may wish to refer to help(gam), and other documentation accompanying the mgcv package. All examples are reproduced and extended from mgcv‘s gam() help pages.

Wood SN (2011). “Fast stable restricted maximum likelihood and marginal likelihood estimation of semiparametric generalized linear models.” Journal of the Royal Statistical Society (B), 73 (1), pp. 3-36.

Wood SN (2004). “Stable and efficient multiple smoothing parameter estimation for generalized additive models.” Journal of the American Statistical Association, 99 (467), pp. 673-686.

Wood S (2006). Generalized Additive Models: An Introduction with R. Chapman and Hall/CRC.

Wood SN (2003). “Thin-plate regression splines.” Journal of the Royal Statistical Society (B), 65 (1), pp. 95-114.

Wood SN (2000). “Modelling and smoothing parameter estimation with multiple quadratic penalties.” Journal of the Royal Statistical Society (B), 62 (2), pp. 413-428.