Warning
ZeligMultilevel is currently under development. We are working on the model vignettes of the package.
zeligmultilevel-logitmixed¶
logit.mixed: Mixed effects logistic Regression
Use generalized multi-level linear regression if you have covariates that are grouped according to one or more classification factors. The logit model is appropriate when the dependent variable is dichotomous.
While generally called multi-level models in the social sciences, this class of models is often referred to as mixed-effects models in the statistics literature and as hierarchical models in a Bayesian setting. This general class of models consists of linear models that are expressed as a function of both fixed effects, parameters corresponding to an entire population or certain repeatable levels of experimental factors, and random effects, parameters corresponding to individual experimental units drawn at random from a population.
Syntax¶
z5 <- zlogitmixed$new()
z5$zelig(formula= y ~ x1 + x2 + (z1 + z2 | g), weights = w, data = mydata)
z5$setx()
z5$sim()
With the Zelig 4 compatibility wrappers:
z.out <- zelig(formula= y ~ x1 + x2 + (z1 + z2 | g),
data = mydata, weights = w, model = "logit.mixed")
x.out <- setx(z.out)
s.out <- sim(z.out, x = x.out)
Inputs¶
zelig() takes the following arguments for multi:
- formula: a two-sided linear formula object describing the systematic component of the model, with the response on the left of a operator and the fixed effects terms, separated by + operators, on the right. Any random effects terms are included with the notation (z1 + ... + zn | g) with z1 + ... + zn specifying the model for the random effects and g the grouping structure. Random intercept terms are included with the notation (1 | g).
Additional Inputs¶
Additionally, users may wish to refer to glmer in the package lme4 for more information, including control parameters for the estimation algorithm and their defaults.
Examples¶
Basic Example with First Differences¶
Attach sample data:
data(voteincome)
Estimate model:
z.out <- zelig(vote ~ education + age + female + (1 | state),
data = voteincome, model = "logit.mixed")
## Warning in readLines(zeligmixedmodels): incomplete final line found on
## '/usr/lib64/R/library/ZeligMultilevel/JSON/zelig5mixedmodels.json'
## How to cite this model in Zelig:
## TBD. 2016.
## logit.mixed:
## in Christine Choirat, James Honaker, Kosuke Imai, Gary King, and Olivia Lau,
## "Zelig: Everyone's Statistical Software," http://zeligproject.org/
Summarize regression coefficients and estimated variance of random effects:
summary(z.out)
## Model:
## Generalized linear mixed model fit by maximum likelihood (Laplace
## Approximation) [glmerMod]
## Family: binomial ( logit )
## Formula: vote ~ education + age + female + (1 | state)
## Data: voteincome
##
## AIC BIC logLik deviance df.resid
## 1213 1239 -601 1203 1495
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -3.731 0.294 0.374 0.446 0.817
##
## Random effects:
## Groups Name Variance Std.Dev.
## state (Intercept) 0.0247 0.157
## Number of obs: 1500, groups: state, 2
##
## Fixed effects:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -0.13996 0.35732 -0.39 0.69530
## education 0.40734 0.07910 5.15 2.6e-07
## age 0.01486 0.00437 3.40 0.00068
## female 0.25009 0.14924 1.68 0.09378
##
## Correlation of Fixed Effects:
## (Intr) eductn age
## education -0.709
## age -0.733 0.286
## female -0.253 0.061 0.003
## Next step: Use 'setx' method
Set explanatory variables to their default values, with high (80th percentile) and low (20th percentile) values for education:
x.high <- setx(z.out, education = quantile(voteincome$education, 0.8))
## [1] "state"
x.low <- setx(z.out, education = quantile(voteincome$education, 0.2))
## [1] "state"
Generate first differences for the effect of high versus low education on voting:
##
## sim x :
## -----
## ev
## mean sd 50% 2.5% 97.5%
## [1,] 0.913 0.0148 0.915 0.88 0.939
## pv
## 0 1
## [1,] 0.084 0.916
##
## sim x1 :
## -----
## ev
## mean sd 50% 2.5% 97.5%
## [1,] 0.824 0.0204 0.825 0.78 0.862
## pv
## 0 1
## [1,] 0.171 0.829
## fd
## mean sd 50% 2.5% 97.5%
## [1,] -0.0893 0.0168 -0.0895 -0.123 -0.0579
s.out <- sim(z.out, x = x.high, x1 = x.low)
summary(s.out)
plot(s.out)
Graphs of Quantities of Interest for Logit Mixed Model
Mixed effects Logistic Regression Model¶
Let be the binary dependent variable, realized for
observation in group 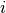 as which takes
the value of either 0 or 1, for ,
.
as which takes
the value of either 0 or 1, for ,
.
The stochastic component is described by a Bernoulli distribution with mean vector .
The -dimensional vector of random effects, , is restricted to be mean zero, and therefore is completely characterized by the variance covarance matrix , a symmetric positive semi-definite matrix.
The systematic component is
where is the array of known fixed effects explanatory variables,
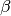 is the
-dimensional vector of fixed effects coefficients,
is the array of known
random effects explanatory variables and is the
-dimensional vector of random effects.
is the
-dimensional vector of fixed effects coefficients,
is the array of known
random effects explanatory variables and is the
-dimensional vector of random effects.
Quantities of Interest¶
The predicted values are draws from the Binomial distribution with mean equal to the simulated expected value, for
given and and simulations of of
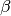 and from their posterior distributions. The
estimated variance covariance matrices are taken as correct and are
themselves not simulated.
and from their posterior distributions. The
estimated variance covariance matrices are taken as correct and are
themselves not simulated.The expected values are simulations of the predicted probability of a success given draws of
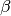 from its
posterior:
from its
posterior:The first difference is given by the difference in predicted probabilities, conditional on and , representing different values of the explanatory variables.
The risk ratio (qi$rr) is defined as
In conditional prediction models, the average predicted treatment effect for the treatment group is given by
where is a binary explanatory variable defining the treatment and control groups. Variation in the simulations is due to uncertainty in simulating , the counterfactual predicted value of for observations in the treatment group, under the assumption that everything stays the same except that the treatment indicator is switched to .
In conditional prediction models, the average expected treatment effect for the treatment group is given by
where is a binary explanatory variable defining the treatment and control groups. Variation in the simulations is due to uncertainty in simulating , the counterfactual expected value of for observations in the treatment group, under the assumption that everything stays the same except that the treatment indicator is switched to .
Output Values¶
The output of each Zelig command contains useful information which you may view. You may examine the available information in z.out by using getters (http://docs.zeligproject.org/en/latest/getters.html), see the fixed effect coefficients by using z.out$getcoef(), and a default summary of information through summary(z.out). Other elements available are listed below.
- From the zelig() output stored in summary(z.out), you may extract:
- fixef: numeric vector containing the conditional estimates of the fixed effects.
- ranef: numeric vector containing the conditional modes of the random effects.
- From the sim() output stored in s.out, you may extract quantities of
interest via getters:
- s.out$getqi(qi = "pv"): the simulated predicted values drawn from the distributions defined by the expected values.
- s.out$getqi(qi = "ev"): the simulated expected values for the specified values of x.
- s.out$getqi(qi = "fd"): the simulated first differences in the expected values for the values specified in x and x1.
- s.out$getqi(treatment): the simulated average predicted treatment effect for the treated from conditional prediction models.
See also¶
Mixed effects linear regression is part of lme4 package.
Bates D, Mächler M, Bolker B and Walker S (2015). “Fitting Linear Mixed-Effects Models Using lme4.” Journal of Statistical Software, 67 (1), pp. 1-48. doi: 10.18637/jss.v067.i01 (URL: http://doi.org/10.18637/jss.v067.i01).