zeligchoice-bprobit¶
Bivariate Probit Regression for Two Dichotomous Dependent Variables
Use the bivariate probit regression model if you have two binary dependent variables , and wish to model them jointly as a function of some explanatory variables. Each pair of dependent variables has four potential outcomes, , , , and . The joint probability for each of these four outcomes is modeled with three systematic components: the marginal Pr and Pr, and the correlation parameter for the two marginal distributions. Each of these systematic components may be modeled as functions of (possibly different) sets of explanatory variables.
Syntax¶
First load packages:
library("Zelig")
library("ZeligChoice")
With reference classes:
z5 <- zbprobit$new()
z5$zelig(cbind(Y1, Y2) ~ X1 + X2 + X3, data = mydata)
z5$setx()
z5$sim()
With the Zelig 4 compatibility wrappers:
z.out <- zelig(cbind(Y1, Y2) ~ X1 + X2 + X3,
model = "bprobit", data = mydata)
x.out <- setx(z.out)
s.out <- sim(z.out, x = x.out, x1 = NULL)
Input Values¶
In every bivariate probit specification, there are three equations which correspond to each dependent variable (, ), and the correlation parameter . Since the correlation parameter does not correspond to one of the dependent variables, the model estimates as a constant by default. Hence, only two formulas (for and ) are required. If the explanatory variables for and are the same and effects are estimated separately for each parameter, you may use the following short hand:
fml <- list(cbind(Y1,Y2) ~ X1 + X2)
which has the same meaning as:
fml <- list(mu1 = Y1 ~ X1 + X2, + mu2 = Y2 ~ X1 + X2)
You may use the function tag() to constrain variables across equations. The tag() function takes a variable and a label for the effect parameter. Below, the constrained effect of x3 in both equations is called the age parameter:
fml <- list(mu1 = y1 ~ x1 + tag(x3, “age”), + mu2 = y2 ~ x2 +
tag(x3, “age”))
You may also constrain different variables across different equations to have the same effect.
Examples¶
Basic Example [basic.bp]¶
Load the data and estimate the model:
data(sanction)
z.out1 <- zelig(cbind(import, export) ~ coop + cost + target,
model = "bprobit", data = sanction)
## How to cite this model in Zelig:
## Thomas W. Yee. 2007.
## bprobit: Bivariate Probit Regression for Dichotomous Dependent Variables
## in Christine Choirat, James Honaker, Kosuke Imai, Gary King, and Olivia Lau,
## "Zelig: Everyone's Statistical Software," http://zeligproject.org/
summary(z.out1)
## Model:
##
## Call:
## z5$zelig(formula = cbind(import, export) ~ coop + cost + target,
## data = sanction)
##
## Pearson residuals:
## Min 1Q Median 3Q Max
## probit(mu1) -2.16 -0.531 -0.253 0.462 2.17
## probit(mu2) -5.11 -0.502 0.059 0.643 2.95
## rhobit(rho) -2.17 -0.418 0.103 0.287 4.30
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept):1 -1.7181 0.6188 -2.78 0.0055
## (Intercept):2 -1.8663 0.6017 -3.10 0.0019
## (Intercept):3 -0.3811 0.4983 -0.76 0.4444
## coop:1 0.1679 0.2010 0.84 0.4035
## coop:2 -0.0284 0.1984 -0.14 0.8863
## cost:1 1.4687 0.3695 3.98 7.0e-05
## cost:2 1.5318 0.3775 4.06 4.9e-05
## target:1 -0.7522 0.2750 -2.74 0.0062
## target:2 -0.2821 0.2553 -1.10 0.2692
##
## Number of linear predictors: 3
##
## Names of linear predictors: probit(mu1), probit(mu2), rhobit(rho)
##
## Dispersion Parameter for binom2.rho family: 1
##
## Log-likelihood: -72 on 225 degrees of freedom
##
## Number of iterations: 5
## Next step: Use 'setx' method
By default, zelig() estimates two effect parameters for each explanatory variable in addition to the correlation coefficient; this formulation is parametrically independent (estimating unconstrained effects for each explanatory variable), but stochastically dependent because the models share a correlation parameter. Generate baseline values for the explanatory variables (with cost set to 1, net gain to sender) and alternative values (with cost set to 4, major loss to sender):
x.low <- setx(z.out1, cost = 1)
x.high <- setx(z.out1, cost = 4)
Simulate fitted values and first differences:
s.out1 <- sim(z.out1, x = x.low, x1 = x.high)
summary(s.out1)
##
## sim x :
## -----
## ev
## mean sd 50% 2.5% 97.5%
## Pr(Y1=0, Y2=0) 0.76441 0.08113 0.77746 5.84e-01 0.894
## Pr(Y1=0, Y2=1) 0.16533 0.07194 0.15715 5.83e-02 0.343
## Pr(Y1=1, Y2=0) 0.06234 0.04313 0.05083 1.04e-02 0.175
## Pr(Y1=1, Y2=1) 0.00792 0.00968 0.00471 9.15e-05 0.037
## pv
## 0 1
## (Y1=0, Y2=0) 0.212 0.788
## (Y1=0, Y2=1) 0.859 0.141
## (Y1=1, Y2=0) 0.937 0.063
## (Y1=1, Y2=1) 0.992 0.008
##
## sim x1 :
## -----
## ev
## mean sd 50% 2.5% 97.5%
## Pr(Y1=0, Y2=0) 1.61e-05 0.000106 1.70e-08 1.57e-11 0.000121
## Pr(Y1=0, Y2=1) 1.48e-02 0.036011 2.17e-03 5.11e-06 0.106903
## Pr(Y1=1, Y2=0) 3.35e-03 0.013915 1.88e-04 4.22e-08 0.024888
## Pr(Y1=1, Y2=1) 9.82e-01 0.037952 9.96e-01 8.85e-01 0.999942
## pv
## 0 1
## (Y1=0, Y2=0) 1.000 0.000
## (Y1=0, Y2=1) 0.989 0.011
## (Y1=1, Y2=0) 0.999 0.001
## (Y1=1, Y2=1) 0.012 0.988
## fd
## mean sd 50% 2.5% 97.5%
## Pr(Y1=0, Y2=0) -0.764 0.0811 -0.7775 -0.894 -0.58406
## Pr(Y1=0, Y2=1) -0.151 0.0823 -0.1443 -0.331 -0.02144
## Pr(Y1=1, Y2=0) -0.059 0.0464 -0.0494 -0.171 -0.00285
## Pr(Y1=1, Y2=1) 0.974 0.0422 0.9888 0.870 0.99934
plot(s.out1)
Graphs of Quantities of Interest for Bivariate Probit
Model¶
For each observation, define two binary dependent variables,
and , each of which take the value of either 0 or 1 (in the
following, we suppress the observation index 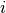 ). We model the
joint outcome , using two marginal
probabilities for each dependent variable, and the correlation
parameter, which describes how the two dependent variables are related.
). We model the
joint outcome , using two marginal
probabilities for each dependent variable, and the correlation
parameter, which describes how the two dependent variables are related.
The stochastic component is described by two latent (unobserved) continuous variables which follow the bivariate Normal distribution:
where is a mean for and is a scalar correlation parameter. The following observation mechanism links the observed dependent variables, , with these latent variables
The systemic components for each observation are
Quantities of Interest¶
For simulations, expected values form an matrix.
The expected values (qi$ev) for the binomial probit model are the predicted joint probabilities. Simulations of , , and (drawn form their sampling distributions) are substituted into the systematic components, to find simulations of the predicted joint probabilities :
where and may take a value of either 0 or 1, is the bivariate Normal density.
The predicted values (qi$pr) are draws from the multinomial distribution given the expected joint probabilities.
The first difference (qi$fd) in each of the predicted joint probabilities are given by
The risk ratio (qi$rr) for each of the predicted joint probabilities are given by
In conditional prediction models, the average expected treatment effect (att.ev) for the treatment group is
where is a binary explanatory variable defining the treatment () and control () groups. Variation in the simulations are due to uncertainty in simulating , the counterfactual expected value of for observations in the treatment group, under the assumption that everything stays the same except that the treatment indicator is switched to .
In conditional prediction models, the average predicted treatment effect (att.pr) for the treatment group is
where is a binary explanatory variable defining the treatment () and control () groups. Variation in the simulations are due to uncertainty in simulating , the counterfactual predicted value of for observations in the treatment group, under the assumption that everything stays the same except that the treatment indicator is switched to .
Output Values¶
The output of each Zelig command contains useful information which you may view. For example, if you run z.out <- zelig(y ~ x, model = bprobit, data), then you may examine the available information in z.out by using names(z.out), see the coefficients by using z.out$coefficients, and obtain a default summary of information through summary(z.out). Other elements available through the $ operator are listed below.
- From the zelig() output object z.out, you may extract:
- coefficients: the named vector of coefficients.
- fitted.values: an matrix of the in-sample fitted values.
- predictors: an matrix of the linear predictors .
- residuals: an matrix of the residuals.
- df.residual: the residual degrees of freedom.
- df.total: the total degrees of freedom.
- rss: the residual sum of squares.
- y: an matrix of the dependent variables.
- zelig.data: the input data frame if save.data = TRUE.
- From summary(z.out), you may extract:
- coef3: a table of the coefficients with their associated standard errors and -statistics.
- cov.unscaled: the variance-covariance matrix.
- pearson.resid: an matrix of the Pearson residuals.
See also¶
The bivariate probit function is part of the VGAM package by Thomas Yee. In addition, advanced users may wish to refer to help(vglm) in the VGAM library.
Yee TW (2015). Vector Generalized Linear and Additive Models: With an Implementation in R. Springer, New York, USA.
Yee TW and Wild CJ (1996). “Vector Generalized Additive Models.” Journal of Royal Statistical Society, Series B, 58 (3), pp. 481-493.
Yee TW (2010). “The VGAM Package for Categorical Data Analysis.” Journal of Statistical Software, 32 (10), pp. 1-34. <URL: http://www.jstatsoft.org/v32/i10/>.
Yee TW and Hadi AF (2014). “Row-column interaction models, with an R implementation.” Computational Statistics, 29 (6), pp. 1427-1445.
Yee TW (2016). VGAM: Vector Generalized Linear and Additive Models. R package version 1.0-2, <URL: http://CRAN.R-project.org/package=VGAM>.
Yee TW (2013). “Two-parameter reduced-rank vector generalized linear models.” Computational Statistics and Data Analysis. <URL: http://ees.elsevier.com/csda>.
Yee TW, Stoklosa J and Huggins RM (2015). “The VGAM Package for Capture-Recapture Data Using the Conditional Likelihood.” Journal of Statistical Software, 65 (5), pp. 1-33. <URL: http://www.jstatsoft.org/v65/i05/>.